91. A man whose eye level is 1.5 metres above the ground observes the angle of elevation of the tower to be $${{{60}^ \circ }}.$$ If the distance of the man from the tower be 10 metres, the height of the tower is
A
$$\left( {1.5 + 10\sqrt 3 } \right)m$$
B
$${10\sqrt 3 } \, m$$
C
$$\left( {1.5 + \frac{{10}}{{\sqrt 3 }}} \right)m$$
D
None of these
Answer :
$$\left( {1.5 + 10\sqrt 3 } \right)m$$
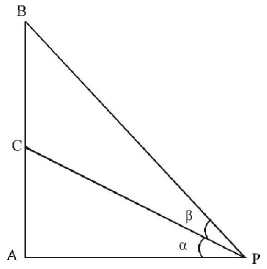
92. Let a vertical tower $$AB$$ have its end $$A$$ on the level ground. Let $$C$$ be the mid - point of $$AB$$ and $$P$$ be a point on the ground such that $$AP = 2AB.$$ If $$\angle BPC = \beta ,$$ then $$\tan\beta $$ is equal to:
A
$$\frac{4}{9}$$
B
$$\frac{6}{7}$$
C
$$\frac{1}{4}$$
D
$$\frac{2}{9}$$
Answer :
$$\frac{2}{9}$$
93.
Let $$PQR$$ be a triangle of area $$\Delta $$ with $$a = 2,b = \frac{7}{2}$$ and $$c = \frac{5}{2},$$ where $$a, b$$ and $$c$$ are the lengths of the sides of the triangle opposite to the angles at $$P, Q$$ and $$R$$ respectively.
Then $$\frac{{2\sin P - \sin 2P}}{{2\sin P + \sin 2P}}$$ equals
A
$$\frac{3}{{4\Delta }}$$
B
$$\frac{45}{{4\Delta }}$$
C
$${\left( {\frac{3}{{4\Delta }}} \right)^2}$$
D
$${\left( {\frac{45}{{4\Delta }}} \right)^2}$$
Answer :
$${\left( {\frac{3}{{4\Delta }}} \right)^2}$$
94. Which of the following pieces of data does NOT uniquely determine an acute-angled triangle $$ABC$$ ($$R$$ being the radius of the circumcircle) ?
A
$$a,\sin A,\sin B$$
B
$$a, b, c$$
C
$$a,\sin B,R$$
D
$$a,\sin A,R$$
Answer :
$$a,\sin A,R$$
95. If in a triangle, $$R$$ and $$r$$ are the circumradius and inradius respectively then the HM of the exradii of the triangle is
A
$$3r$$
B
$$2R$$
C
$$R + r$$
D
None of these
Answer :
$$3r$$
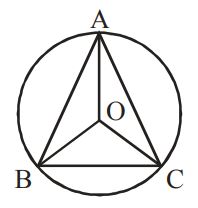
96. If the radius of the circumcircle of isosceles triangle $$ABC$$ is equal to $$AB = AC,$$ then the angle $$A$$ is :
A
$${30^ \circ }$$
B
$${60^ \circ }$$
C
$${90^ \circ }$$
D
$${120^ \circ }$$
Answer :
$${120^ \circ }$$
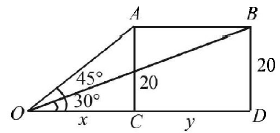
97. A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point $$O$$ on the ground is 45°. It flies off horizontally straight away from the point $$O.$$ After one second, the elevation of the bird from $$O$$ is reduced to 30°. Then the speed (in $$m/s$$ ) of the bird is
A
$$20\sqrt 2 $$
B
$$20\left( {\sqrt 3 - 1} \right)$$
C
$$40\left( {\sqrt 2 - 1} \right)$$
D
$$40\left( {\sqrt 3 - \sqrt 2 } \right)$$
Answer :
$$20\left( {\sqrt 3 - 1} \right)$$
98. $$AB$$ is a vertical pole with $$B$$ at the ground level and $$A$$ at the top. A man finds that the angle of elevation of the point $$A$$ from a certain point $$C$$ on the ground is 60°. He moves away from the pole along the line $$BC$$ to a point $$D$$ such that $$CD = 7 m.$$ From $$D$$ the angle of elevation of the point $$A$$ is 45°. Then the height of the pole is
A
$$\frac{{7\sqrt 3 }}{2}\frac{1}{{\sqrt 3 - 1}}m$$
B
$$\frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 + 1} \right)m$$
C
$$\frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 - 1} \right)m$$
D
$$\frac{{7\sqrt 3 }}{2}\frac{1}{{\sqrt 3 + 1}}m$$
Answer :
$$\frac{{7\sqrt 3 }}{2}\left( {\sqrt 3 + 1} \right)m$$
99. In a $$\vartriangle ABC,R = $$ circumradius and $$r =$$ inradius. The value of $$\frac{{a\cos A + b\cos B + c\cos C}}{{a + b + c}}$$ is equal to
A
$$\frac{R}{r}$$
B
$$\frac{R}{2r}$$
C
$$\frac{r}{R}$$
D
$$\frac{2r}{R}$$
Answer :
$$\frac{r}{R}$$
100. $$A, B, C$$ are the angles of a triangle, then $${\sin ^2}A + {\sin ^2}B + {\sin ^2}C - 2\cos A\cos B\cos C = $$
A
1
B
2
C
3
D
4
Answer :
2