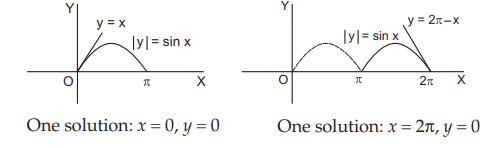61.
If $$\left[ {{{\sin }^{ - 1}}{{\cos }^{ - 1}}{{\sin }^{ - 1}}{{\tan }^{ - 1}}x} \right] = 1,$$ where [.] denotes the greatest integer function, then $$x$$ belongs to the interval A
$$\left[ {\tan \sin \cos 1,\tan \sin \cos \sin 1} \right]$$
B
$$\left( {\tan \sin \cos 1,\tan \sin \cos \sin 1} \right)$$
C
$$\left[ {- 1, 1} \right]$$
D
$$\left[ {\sin \cos \tan 1,\sin \cos \sin \tan 1} \right]$$
Answer :
$$\left[ {\tan \sin \cos 1,\tan \sin \cos \sin 1} \right]$$
View Solution
Discuss Question
$$\eqalign{
& {\text{We have}},1 \leqslant {\sin ^{ - 1}}{\cos ^{ - 1}}{\sin ^{ - 1}}{\tan ^{ - 1}}x \leqslant \frac{\pi }{2} \cr
& \Rightarrow \sin 1 \leqslant {\cos ^{ - 1}}{\sin ^{ - 1}}{\tan ^{ - 1}}x \leqslant 1 \cr
& \Rightarrow \cos \sin 1 \geqslant {\sin ^{ - 1}}{\tan ^{ - 1}}x \geqslant \cos 1 \cr
& \Rightarrow \sin \cos \sin 1 \geqslant {\tan ^{ - 1}}x \geqslant \sin \cos 1 \cr
& \Rightarrow \tan \sin \cos \sin 1 \geqslant x \geqslant \tan \sin \cos 1 \cr
& \therefore x \in \left[ {\tan \sin \cos 1,\tan \sin \cos \sin 1} \right] \cr} $$
62.
The number of real solutions of $$\left( {x,y} \right),$$ where $$\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left( {\cos x} \right), - 2\pi \leqslant x \leqslant 2\pi ,$$ is A
2
B
1
C
3
D
4
Answer :
3
View Solution
Discuss Question
$$\eqalign{
& {\text{In }}\left[ {0,\pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left( {\cos x} \right) = x. \cr
& {\text{In }}\left[ {\pi ,2\pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( {2\pi - x} \right)} \right\} = 2\pi - x. \cr
& {\text{In }}\left[ { - \pi ,0} \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( { - x} \right)} \right\} = - x. \cr
& {\text{In }}\left[ { - 2\pi , - \pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( {2\pi + x} \right)} \right\} = 2\pi + x. \cr} $$
Plotting the graphs, we have,
∴ there are 3 solutions $$\left( {0,0} \right),\left( {2\pi ,0} \right),\left( { - 2\pi ,0} \right).$$
63.
If $${\cos ^{ - 1}}\lambda + {\cos ^{ - 1}}\mu + {\cos ^{ - 1}}\gamma = 3\pi ,$$ then the value of $$\lambda \mu + \mu \gamma + \gamma \lambda $$ is A
0
B
1
C
3
D
6
Answer :
3
View Solution
Discuss Question
We know that $$0 \leqslant {\cos ^{ - 1}}x \leqslant \pi .$$
64.
The sum to the $$n$$ term of the series $${\text{cose}}{{\text{c}}^{ - 1}}\sqrt {10} + {\text{cose}}{{\text{c}}^{ - 1}}\sqrt {50} + {\text{cose}}{{\text{c}}^{ - 1}}\sqrt {170} + ..... + {\text{cose}}{{\text{c}}^{ - 1}}\sqrt {\left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right)} {\text{ is}}$$ A
$${\tan ^{ - 1}}\left( {n + 1} \right) - \frac{\pi }{4}$$
B
$$\frac{\pi }{4}$$
C
$${\tan ^{ - 1}}\left( {n + 1} \right)$$
D
$$1$$
Answer :
$${\tan ^{ - 1}}\left( {n + 1} \right) - \frac{\pi }{4}$$
View Solution
Discuss Question
$$\eqalign{
& {\text{Let, }}\theta = {\text{cose}}{{\text{c}}^{ - 1}}\sqrt {\left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right)} \cr
& \Rightarrow {\text{cose}}{{\text{c}}^2}\theta = \left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right) \cr
& = {\left( {{n^2} + 1} \right)^2} + 2n\left( {{n^2} + 1} \right) + {n^2} + 1 \cr
& = {\left( {{n^2} + n + 1} \right)^2} + 1 \cr
& \Rightarrow {\cot ^2}\theta = {\left( {{n^2} + n + 1} \right)^2} \cr
& \Rightarrow \tan \theta = \frac{1}{{{n^2} + n + 1}} = \frac{{\left( {n + 1} \right) - n}}{{1 + \left( {n + 1} \right)n}} \cr
& \Rightarrow \theta = {\tan ^{ - 1}}\left[ {\frac{{\left( {n + 1} \right) - n}}{{1 + \left( {n + 1} \right)n}}} \right] = {\tan ^{ - 1}}\left( {n + 1} \right) - {\tan ^{ - 1}}n \cr} $$
65.
The formula $${\sin ^{ - 1}}\left\{ {2x\left( {1 - {x^2}} \right)} \right\} = 2\,{\sin ^{ - 1}}x$$ is true for all values of $$x$$ lying in the interval A
$$\left[ { - 1,1} \right]$$
B
$$\left[ { 0,1} \right]$$
C
$$\left[ { - 1,0} \right]$$
D
$$\left[ { - \frac{1}{{\sqrt 2 }},\frac{1}{{\sqrt 2 }}} \right]$$
Answer :
$$\left[ { - \frac{1}{{\sqrt 2 }},\frac{1}{{\sqrt 2 }}} \right]$$
View Solution
Discuss Question
$${\sin ^{ - 1}}\left\{ {2x\left( {1 - {x^2}} \right)} \right\} = 2\,{\sin ^{ - 1}}x$$ is true $$\forall x \in \left[ { - \frac{1}{{\sqrt 2 }},\frac{1}{{\sqrt 2 }}} \right]$$
66.
The sum of the infinite series $${\sin ^{ - 1}}\left( {\frac{1}{{\sqrt 2 }}} \right) + {\sin ^{ - 1}}\left( {\frac{{\sqrt 2 - 1}}{{\sqrt 6 }}} \right) + {\sin ^{ - 1}}\left( {\frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt {12} }}} \right) + ..... + ..... + {\sin ^{ - 1}}\left( {\frac{{\sqrt n - \sqrt {\left( {n - 1} \right)} }}{{\sqrt {\left\{ {n\left( {n + 1} \right)} \right\}} }}} \right) + .....$$ is A
$$\frac{\pi }{8}$$
B
$$\frac{\pi }{4}$$
C
$$\frac{\pi }{2}$$
D
$$\pi$$
Answer :
$$\frac{\pi }{2}$$
View Solution
Discuss Question
$$\eqalign{
& \because {T_r} = {\sin ^{ - 1}}\left( {\frac{{\sqrt r - \sqrt {\left( {r - 1} \right)} }}{{\sqrt {r\left( {r + 1} \right)} }}} \right) \cr
& = {\tan ^{ - 1}}\left( {\frac{{\sqrt r - \sqrt {\left( {r - 1} \right)} }}{{1 + \sqrt r \sqrt {\left( {r - 1} \right)} }}} \right) \cr
& {S_n} = \sum\limits_{r = 1}^n {{{\tan }^{ - 1}}\left( {\frac{{\sqrt r - \sqrt {\left( {r - 1} \right)} }}{{1 + \sqrt r \sqrt {\left( {r - 1} \right)} }}} \right)} \cr
& = \sum\limits_{r = 1}^n {\left\{ {{{\tan }^{ - 1}}\sqrt r - {{\tan }^{ - 1}}\sqrt {\left( {r - 1} \right)} } \right\}} \cr
& = {\tan ^{ - 1}}\sqrt n - {\tan ^{ - 1}}\sqrt 0 = {\tan ^{ - 1}}\sqrt n - 0 \cr
& \therefore {S_\infty } = {\tan ^{ - 1}}\infty = \frac{\pi }{2} \cr} $$
67.
If $${\sin ^{ - 1}}\left( {\frac{{2a}}{{1 + {a^2}}}} \right) - {\cos ^{ - 1}}\left( {\frac{{1 - {b^2}}}{{1 + {b^2}}}} \right) = {\tan ^{ - 1}}\left( {\frac{{2x}}{{1 - {x^2}}}} \right),$$ then what is the value of $$x\,?$$ A
$$\frac{a}{b}$$
B
$$ab$$
C
$$\frac{b}{a}$$
D
$$\frac{{a - b}}{{1 + ab}}$$
Answer :
$$\frac{{a - b}}{{1 + ab}}$$
View Solution
Discuss Question
Given,
68.
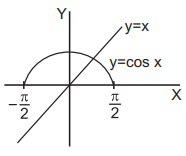
The number of real solutions of the equation $$\sqrt {1 + \cos 2x} = \sqrt 2 \,{\sin ^{ - 1}}\left( {\sin x} \right), - \pi \leqslant x \leqslant \pi ,$$ is A
0
B
1
C
2
D
infinite
Answer :
2
View Solution
Discuss Question
Here, $$\left| {\cos x} \right| = {\sin ^{ - 1}}\left( {\sin x} \right).$$
If, $$ - \frac{\pi }{2} \leqslant x \leqslant \frac{\pi }{2}\,{\text{then}}\,\,\cos x = x.$$
In the case there is one solution, obtained graphically.
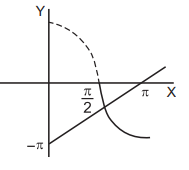
If, $$\frac{\pi }{2} < x \leqslant \pi $$ then $$ - \cos x = {\sin ^{ - 1}}\left\{ {\sin \left( {\pi - x} \right)} \right\} = \pi - x.$$
$$\therefore \,\,\cos x = x - \pi .$$
In this case there is one solution, obtained graphically.
If, $$ - \pi \leqslant x < - \frac{\pi }{2}$$ then $$ - \cos x = {\sin ^{ - 1}}\left\{ {\sin \left( { - \pi - x} \right)} \right\} = - x - \pi ,\,{\text{i}}{\text{.e}}{\text{.,}}\cos x = x + \pi .$$
This gives no solution as can be seen from their graphs.
69.
If $${\cot ^{ - 1}}\frac{n}{\pi } > \frac{\pi }{6},n \in N,$$ then the maximum value of $$n$$ is A
1
B
5
C
9
D
None of these
Answer :
5
View Solution
Discuss Question
$$\eqalign{
& {\cot ^{ - 1}}\frac{n}{\pi } > \frac{\pi }{6} \cr
& \Rightarrow \,\,\cot \left( {{{\cot }^{ - 1}}\frac{n}{\pi }} \right) < \cot \frac{\pi }{6} \cr
& \Rightarrow \,\,\frac{n}{\pi } < \sqrt 3 \cr
& \Rightarrow \,\,n < \sqrt 3 \pi = 5.5\left( {{\text{nearly}}} \right). \cr} $$
70.
If $${\sin ^{ - 1}}1 + {\sin ^{ - 1}}\frac{4}{5} = {\sin ^{ - 1}}x,$$ then what is $$x$$ equal to ? A
$$\frac{3}{5}$$
B
$$\frac{4}{5}$$
C
$$1$$
D
$$0$$
Answer :
$$\frac{3}{5}$$
View Solution
Discuss Question
$$\eqalign{
& {\text{Let,}}\,\,{\sin ^{ - 1}}\left( 1 \right) + {\sin ^{ - 1}}\left( {\frac{4}{5}} \right) = {\sin ^{ - 1}}x \cr
& {\text{Let,}}\,\,{\sin ^{ - 1}}\left( 1 \right) = \theta \cr
& \Rightarrow \sin \theta = 1 \cr
& \Rightarrow \cos \theta = 0\,\,{\text{and }}{\sin ^{ - 1}}\left( {\frac{4}{5}} \right) = \phi \cr
& \Rightarrow \sin \phi = \left( {\frac{4}{5}} \right) \cr
& \Rightarrow \cos \phi = \sqrt {1 - \frac{{16}}{{25}}} = \sqrt {\frac{9}{{25}}} = \frac{3}{5} \cr
& \therefore {\sin ^{ - 1}}x = \theta + \phi \cr
& \Rightarrow x = \sin \left( {\theta + \phi } \right) = \sin \theta \cos \phi + \cos \theta \sin \phi \cr
& = 1 \times \frac{3}{5} + 0 \times \frac{4}{5} \cr
& \Rightarrow x = \frac{3}{5} \cr} $$