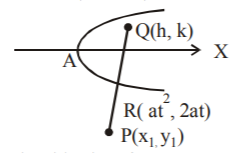31. A line $$PQ$$ meets the parabola $${y^2} = 4ax$$ in $$R$$ such that $$PQ$$ is bisected at $$R$$. If the coordinates of $$P$$ are $$\left( {{x_1},\,{y_1}} \right)$$ then the locus of $$Q$$ is the parabola :
A
$${\left( {y + {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
B
$${\left( {y - {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
C
$${\left( {y + {y_1}} \right)^2} = 8a\left( {x - {x_1}} \right)$$
D
None of these
Answer :
$${\left( {y + {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
32. The normal at the point $$\left( {bt_1^2,\,2b{t_1}} \right)$$ on a parabola meets the parabola again in the point $$\left( {bt_2^2,\,2b{t_2}} \right),$$ then :
A
$${t_2} = {t_1} + \frac{2}{{{t_1}}}$$
B
$${t_2} = - {t_1} - \frac{2}{{{t_1}}}$$
C
$${t_2} = - {t_1} + \frac{2}{{{t_1}}}$$
D
$${t_2} = {t_1} - \frac{2}{{{t_1}}}$$
Answer :
$${t_2} = - {t_1} - \frac{2}{{{t_1}}}$$
33. A chord $$PP'$$ of a parabola cuts the axis of the parabola at $$O$$. The feet of the perpendiculars from $$P$$ and $$P'$$ on the axis are $$M$$ and $$M'$$ respectively. If $$V$$ is the vertex then $$VM,\,VO,\,VM'$$ are in :
A
AP
B
GP
C
HP
D
none of these
Answer :
GP
34. The circle $${x^2} + {y^2} + 2\lambda x = 0,\,\lambda \, \in \,R,$$ touches the parabola $${y^2} = 4x$$ externally. Then :
A
$$\lambda > 0$$
B
$$\lambda < 0$$
C
$$\lambda > 1$$
D
none of these
Answer :
$$\lambda > 0$$
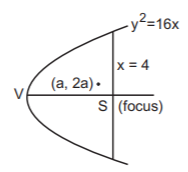
35. The point $$\left( {a,\,2a} \right)$$ is an interior point of the region bounded by the parabola $${y^2} = 16x$$ and the double ordinate through the focus. Then $$a$$ belongs to the open interval :
A
$$a < 4$$
B
$$0 < a < 4$$
C
$$0 < a < 2$$
D
$$a > 4$$
Answer :
$$0 < a < 4$$
36. The locus of a point from which tangents to a parabola are at right angles is a :
A
straight line
B
pair of straight lines
C
circle
D
parabola
Answer :
straight line
37. $$'{t_1}'$$ and $$'{t_2}'$$ are two points on the parabola $${y^2} = 4x.$$ If the chord joining them is a normal to the parabola at $$'{t_1}'$$ then :
A
$${t_1} + {t_2} = 0$$
B
$${t_1}\left( {{t_1} + {t_2}} \right) = 1$$
C
$${t_1}\left( {{t_1} + {t_2}} \right) + 2 = 0$$
D
$${t_1}{t_2} + 1 = 0$$
Answer :
$${t_1}\left( {{t_1} + {t_2}} \right) + 2 = 0$$
38. The length of a focal chord of the parabola $${y^2} = 4ax$$ at a distance $$b$$ from the vertex is $$c.$$ Then :
A
$$2{a^2} = bc$$
B
$${a^3} = {b^2}c$$
C
$$ac = {b^2}$$
D
$${b^2}c = 4{a^3}$$
Answer :
$${b^2}c = 4{a^3}$$
39. The parabola $${y^2} = kx$$ makes an intercept of length 4 on the line $$x - 2y = 1.$$ Then $$k$$ is :
A
$$\frac{{\sqrt {105} - 5}}{{10}}$$
B
$$\frac{{5 - \sqrt {105} }}{{10}}$$
C
$$\frac{{5 + \sqrt {105} }}{{10}}$$
D
none of these
Answer :
$$\frac{{\sqrt {105} - 5}}{{10}}$$
40. The tangents to the parabola $${y^2} = 4x$$ at the points $$\left( {1,\,2} \right)$$ and $$\left( {4,\,4} \right)$$ meet on the line :
A
$$x = 3$$
B
$$x + y = 4$$
C
$$y = 3$$
D
none of these
Answer :
$$y = 3$$