11. Tangent and normal are drawn at $$P\left( {16,\,16} \right)$$ on the parabola $${y^2} = 16x,$$ which intersect the axis of the parabola at $$A$$ and $$B,$$ respectively. If $$C$$ is the centre of the circle through the points $$P,\,A$$ and $$B$$ and $$\angle CPB = \theta ,$$ then a value of $$\tan \,\theta $$ is :
A
$$2$$
B
$$3$$
C
$$\frac{4}{3}$$
D
$$\frac{1}{2}$$
Answer :
$$2$$
12. Two common tangents to the circle $${x^2} + {y^2} = 2{a^2}$$ and parabola $${y^2} = 8ax$$ are-
A
$$x = \pm \left( {y + 2a} \right)$$
B
$$y = \pm \left( {x + 2a} \right)$$
C
$$x = \pm \left( {y + a} \right)$$
D
$$y = \pm \left( {x + a} \right)$$
Answer :
$$y = \pm \left( {x + 2a} \right)$$
13. If the focus of a parabola is $$\left( { - 2,\,1} \right)$$ and the directrix has the equation $$x + y = 3$$ then the vertex is :
A
$$\left( {0,\,3} \right)$$
B
$$\left( { - 1,\,\frac{1}{2}} \right)$$
C
$$\left( { - 1,\,2} \right)$$
D
$$\left( {2,\, - 1} \right)$$
Answer :
$$\left( { - 1,\,2} \right)$$
14. Let $$P,\,Q,\,R$$ be three points on a parabola, normals at which are concurrent. The centroid of the $$\Delta PQR$$ must lie on :
A
a line parallel to the directrix
B
the axis of the parabola
C
a line of slope 1 passing through the vertex
D
none of these
Answer :
the axis of the parabola
15.
Given : A circle, $$2{x^2} + 2{y^2} = 5$$ and a parabola, $${y^2} = 4\sqrt 5 x.$$
Statement-1 : An equation of a common tangent to these curves is $$y = x + \sqrt 5 .$$
Statement-2 : If the line, $$y = mx + \frac{{\sqrt 5 }}{m}\,\left( {m \ne 0} \right)$$ is their common tangent, then $$m$$ satisfies $${m^4} - 3{m^2} + 2 = 0.$$
A
Statement-1 is true; Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
B
Statement-1 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
C
Statement-1 is true; Statement-2 is false.
D
Statement-1 is false; Statement-2 is true.
Answer :
Statement-1 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
16. The locus of the point of intersection of two tangents to the parabola $${y^2} = 4ax,$$ which are at right angle to one another is :
A
$${x^2} + {y^2} = {a^2}$$
B
$$a{y^2} = x$$
C
$$x + a = 0$$
D
$$x + y \pm a = 0$$
Answer :
$$x + a = 0$$
17. The equation $${x^2} + 4xy + 4{y^2} - 3x - 6y - 4 = 0$$ represents a :
A
circle
B
parabola
C
a pair of lines
D
none of these
Answer :
a pair of lines
18. The locus of the middle points of chords of the parabola $${y^2} = 8x$$ drawn through the vertex is a parabola whose :
A
focus is $$\left( {2,\,0} \right)$$
B
latus rectum $$ = 8$$
C
focus is $$\left( {0,\,2} \right)$$
D
latus rectum $$ = 4$$
Answer :
latus rectum $$ = 4$$
19. Through the vertex $$O$$ of a parabola $${y^2} = 4x,$$ chords $$OP$$ and $$OQ$$ are drawn at right angles to one another. The locus of the middle point of $$PQ$$ is :
A
$${y^2} = 2x + 8$$
B
$${y^2} = x + 8$$
C
$${y^2} = 2x - 8$$
D
$${y^2} = x - 8$$
Answer :
$${y^2} = 2x - 8$$
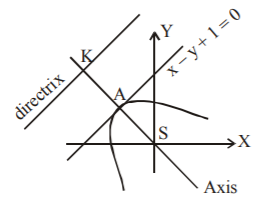
20. The equation of the parabola whose focus is $$\left( {0,\,0} \right)$$ and the tangent at the vertex is $$x - y + 1 = 0$$ is :
A
$${x^2} + {y^2} + 2xy - 4x + 4y - 4 = 0$$
B
$${x^2} - 4x + 4y - 4 = 0$$
C
$${y^2} - 4x + 4y - 4 = 0$$
D
$$2{x^2} + 2{y^2} - 4xy - x + y - 4 = 0$$
Answer :
$${x^2} + {y^2} + 2xy - 4x + 4y - 4 = 0$$