51.
Which one of the following is correct ?
The eccentricity of the conic $$\frac{{{x^2}}}{{{a^2} + \lambda }} + \frac{{{y^2}}}{{{b^2} + \lambda }} = 1,\,\left( {\lambda \geqslant 0} \right)$$
A
increases with increase in $$\lambda $$
B
decreases with increase in $$\lambda $$
C
does not change with $$\lambda $$
D
None of the above
Answer :
decreases with increase in $$\lambda $$
52. $$P$$ is a variable point on the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 2$$ whose foci are $${F_1}$$ and $${F_2}.$$ The maximum area $$\left( {{\text{in uni}}{{\text{t}}^2}} \right)$$ of the $$\Delta PFF'$$ is :
A
$$2b\sqrt {{a^2} - {b^2}} $$
B
$$\sqrt 2 b\sqrt {{a^2} - {b^2}} $$
C
$$b\sqrt {{a^2} - {b^2}} $$
D
$$2a\sqrt {{a^2} - {b^2}} $$
Answer :
$$2b\sqrt {{a^2} - {b^2}} $$
53. Let $$E$$ be the ellipse $$\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1$$ and $$C$$ be the circle $${x^2} + {y^2} = 9.$$ Let $$P = \left( {1,\,2} \right)$$ and $$Q = \left( {2,\,1} \right).$$ Which one of the following is correct ?
A
$$Q$$ lies inside $$C$$ but outside $$E$$
B
$$Q$$ lies outside both $$C$$ and $$E$$
C
$$P$$ lies inside both $$C$$ and $$E$$
D
$$P$$ lies inside $$C$$ but outside $$E$$
Answer :
$$P$$ lies inside $$C$$ but outside $$E$$
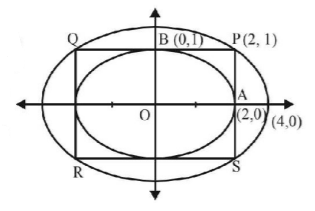
54. The ellipse $${x^2} + 4{y^2} = 4$$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point $$\left( {4,\,0} \right).$$ Then the equation of the ellipse is :
A
$${x^2} + 12{y^2} = 16$$
B
$$4{x^2} + 48{y^2} = 48$$
C
$$4{x^2} + 64{y^2} = 48$$
D
$${x^2} + 16{y^2} = 16$$
Answer :
$${x^2} + 12{y^2} = 16$$
55. If tangents are drawn to the ellipse $${x^2} + 2{y^2} = 2,$$ then the locus of the mid-point of the intercept made by the tangents between the coordinate axes is-
A
$$\frac{1}{{2{x^2}}} + \frac{1}{{4{y^2}}} = 1$$
B
$$\frac{1}{{4{x^2}}} + \frac{1}{{2{y^2}}} = 1$$
C
$$\frac{{{x^2}}}{2} + \frac{{{y^2}}}{4} = 1$$
D
$$\frac{{{x^2}}}{4} + \frac{{{y^2}}}{2} = 1$$
Answer :
$$\frac{1}{{2{x^2}}} + \frac{1}{{4{y^2}}} = 1$$
56. A point on the ellipse $$\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1$$ at a distance equal to the mean of the lengths of the semi-major axis and semi-minor axis from the centre is :
A
$$\left( {\frac{{2\sqrt {91} }}{7},\,\frac{{3\sqrt {105} }}{{14}}} \right)$$
B
$$\left( {\frac{{2\sqrt {91} }}{7},\, - \frac{{3\sqrt {105} }}{{14}}} \right)$$
C
$$\left( {\frac{{2\sqrt {105} }}{7},\,\frac{{3\sqrt {91} }}{{14}}} \right)$$
D
$$\left( { - \frac{{2\sqrt {105} }}{7}, - \,\frac{{3\sqrt {91} }}{{14}}} \right)$$
Answer :
$$\left( {\frac{{2\sqrt {91} }}{7},\,\frac{{3\sqrt {105} }}{{14}}} \right)$$
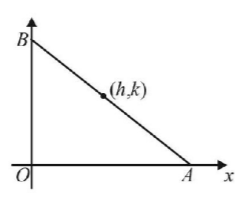
57. The minimum area of triangle formed by the tangent to the $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ & coordinate axes is-
A
$$ab\,\,{\text{sq}}{\text{. units}}$$
B
$$\frac{{{a^2} + {b^2}}}{2}\,\,{\text{sq}}{\text{. units}}$$
C
$$\frac{{{{\left( {a + b} \right)}^2}}}{2}\,\,{\text{sq}}{\text{. units}}$$
D
$$\frac{{{a^2} + ab + {b^2}}}{3}\,\,{\text{sq}}{\text{. units}}$$
Answer :
$$ab\,\,{\text{sq}}{\text{. units}}$$
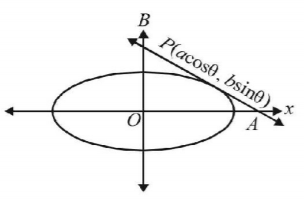
58. The line passing through the extremity $$A$$ of the major axis and the extremity $$B$$ of the minor axis of the ellipse $${x^2} + 9{y^2} = 9$$ meets its auxiliary circle at the point $$M.$$ Then the area of the triangle with vertices $$A,\,M$$ and the origin $$O$$ is :
A
$$\frac{{31}}{{10}}$$
B
$$\frac{{29}}{{10}}$$
C
$$\frac{{21}}{{10}}$$
D
$$\frac{{27}}{{10}}$$
Answer :
$$\frac{{27}}{{10}}$$
59. The value of $$c$$ for which the line $$y = 3x + c$$ touches the ellipse $$16{x^2} + {y^2} = 16$$ is :
A
5
B
1
C
4
D
3
Answer :
5
60. If the ellipse $$9{x^2} + 16{y^2} = 144$$ intercepts the line $$3x + 4y = 12,$$ then what is the length of the chord so formed ?
A
$$5$$ units
B
$$6$$ units
C
$$8$$ units
D
$$10$$ units
Answer :
$$5$$ units