11. The set of real values of $$k$$ for which the equation $$\left( {k + 1} \right){x^2} + 2\left( {k - 1} \right)xy + {y^2} - x + 2y + 3 = 0$$ represents an ellipse is :
A
$$\left( {0,\,3} \right)$$
B
$$\left( { - \infty ,\,0} \right)$$
C
$$\left( {3,\, + \infty } \right)$$
D
$$\left( { - \infty ,\,\infty } \right)$$
Answer :
$$\left( {0,\,3} \right)$$
12. Let $${S_1},\,{S_2}$$ be the foci of the ellipse $$\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{8} = 1.$$ If $$A\left( {x + y} \right)$$ is any point on the ellipse, then the maximum area of the triangle $$A{S_1}{S_2}$$ (in square units) is :
A
$$2\sqrt 2 $$
B
$$2\sqrt 3 $$
C
$$8$$
D
$$4$$
Answer :
$$8$$
13. The tangent to the ellipse $$16{x^2} + 9{y^2} = 144,$$ making equal intercepts on both the axes, is :
A
$$y = x + 3$$
B
$$y = x - 2$$
C
$$x + y = 5$$
D
$$y = - x + 4$$
Answer :
$$x + y = 5$$
14. The equation of the circle passing through the foci of the ellipse $$\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1,$$ and having centre at $$\left( {0,\,3} \right)$$ is :
A
$${x^2} + {y^2} - 6y - 7 = 0$$
B
$${x^2} + {y^2} - 6y + 7 = 0$$
C
$${x^2} + {y^2} - 6y - 5 = 0$$
D
$${x^2} + {y^2} - 6y + 5 = 0$$
Answer :
$${x^2} + {y^2} - 6y - 7 = 0$$
15. If the latus rectum of an ellipse is equal to one half its minor axis, what is the eccentricity of the ellipse ?
A
$$\frac{1}{2}$$
B
$$\frac{{\sqrt 3 }}{2}$$
C
$$\frac{3}{4}$$
D
$$\frac{{\sqrt {15} }}{4}$$
Answer :
$$\frac{{\sqrt 3 }}{2}$$
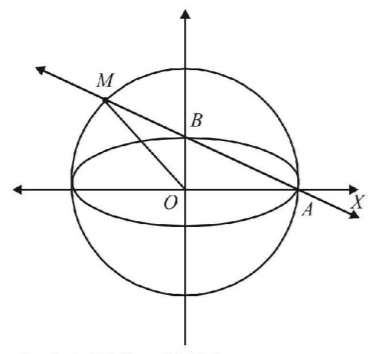
16. The line passing through the extremity $$A$$ of the major axis and extremity $$B$$ of the minor axis of the ellipse $${x^2} + 9{y^2} = 9$$ meets its auxiliary circle at the point $$M.$$ Then the area of the triangle with vertices at $$A,\,M$$ and the origin $$O$$ is-
A
$$\frac{{31}}{{10}}$$
B
$$\frac{{29}}{{10}}$$
C
$$\frac{{21}}{{10}}$$
D
$$\frac{{27}}{{10}}$$
Answer :
$$\frac{{27}}{{10}}$$
17. The centre of the conic section $$14{x^2} - 4xy + 11{y^2} - 44x - 58y + 71 = 0$$ is :
A
$$\left( {2,\,3} \right)$$
B
$$\left( {2,\, - 3} \right)$$
C
$$\left( { - 2,\,3} \right)$$
D
$$\left( { - 2,\, - 3} \right)$$
Answer :
$$\left( {2,\,3} \right)$$
18. If $$P$$ and $$Q$$ are the ends of a pair of conjugate diameters and $$C$$ is the centre of the ellipse $$4{x^2} + 9{y^2} = 36$$ then the area of the $$\Delta CPQ$$ is :
A
$$6\,{\text{uni}}{{\text{t}}^2}$$
B
$$3\,{\text{uni}}{{\text{t}}^2}$$
C
$$2\,{\text{uni}}{{\text{t}}^2}$$
D
$$12\,{\text{uni}}{{\text{t}}^2}$$
Answer :
$$3\,{\text{uni}}{{\text{t}}^2}$$
19. The latus rectum of the conic section $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ whose eccentricity $$ = e,$$ is :
A
$$\frac{{2{a^2}}}{b}$$
B
$$\frac{{2b}}{{{a^2}}}$$
C
$$2a\left( {1 - {e^2}} \right)$$
D
$$2b\left( {1 - {e^2}} \right)$$
Answer :
$$2a\left( {1 - {e^2}} \right)$$
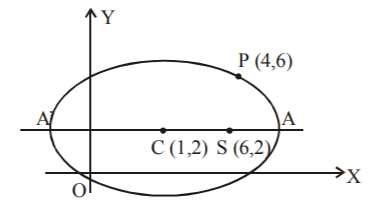
20. The equation of the ellipse with its centre at $$\left( {1,\,2} \right),$$ focus at $$\left( {6,\,2} \right)$$ and passing through the point $$\left( {4,\,6} \right)$$ is $$\frac{{{{\left( {x - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{{b^2}}} = 1,$$ then :
A
$${a^2} = 1,\,{b^2} = 25$$
B
$${a^2} = 25,\,{b^2} = 20$$
C
$${a^2} = 20,\,{b^2} = 25$$
D
None of these
Answer :
None of these