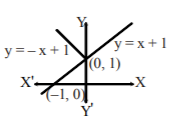71. If $$f\left( x \right) = \frac{{\left[ x \right]}}{{\left| x \right|}},\,x \ne 0$$ where $$\left[ \cdot \right]$$ denotes the greatest integer function, then $$f'\left( 1 \right)$$ is :
A
$$-1$$
B
$$\infty $$
C
nonexistent
D
none of these
Answer :
nonexistent
72. If $$t\left( {1 + {x^2}} \right) = x$$ and $${x^2} + {t^2} = y$$ then $$\frac{{dy}}{{dx}}$$ at $$x=2$$ is :
A
$$\frac{{88}}{{125}}$$
B
$$\frac{{488}}{{125}}$$
C
1
D
none of these
Answer :
$$\frac{{488}}{{125}}$$
73. There exists a function $$f\left( x \right)$$ satisfying $$f\left( 0 \right) = 1,\,f'\left( 0 \right) - 1,\,f\left( x \right) > 0$$ for all $$x$$ and
A
$$f'\left( x \right) < 0$$ for all $$x$$
B
$$ - 1 < f''\left( x \right) < 0$$ for all $$x$$
C
$$ - 2 \leqslant f''\left( x \right) \leqslant - 1$$ for all $$x$$
D
$$f''\left( x \right) \leqslant - 2$$ for all $$x$$
Answer :
$$f'\left( x \right) < 0$$ for all $$x$$
74. The number of points of non-differentiability for $$f\left( x \right) = \max \left\{ {\left| {\left| x \right| - 1} \right|,\,\frac{1}{2}} \right\}$$ is :
A
4
B
3
C
2
D
5
Answer :
5
75. If $$f'\left( x \right) = \sqrt {2{x^2} - 1} $$ and $$y = f\left( {{x^2}} \right)$$ then $$\frac{{dy}}{{dx}}$$ at $$x=1$$ is :
A
2
B
1
C
$$-2$$
D
none of these
Answer :
2
76. $$\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {2h + 2 + {h^2}} \right) - f\left( 2 \right)}}{{f\left( {h - {h^2} + 1} \right) - f\left( 1 \right)}},$$ given that $$f'\left( 2 \right) = 6$$ and $$f'\left( 1 \right) = 4$$
A
does not exist
B
is equal to $$ - \frac{3}{2}$$
C
is equal to $$\frac{3}{2}$$
D
is equal to $$3$$
Answer :
is equal to $$3$$
77. Let $$f:R \to R$$ be a function defined by $$f\left( x \right) = \min \left\{ {x + 1,\,\left| x \right| + 1} \right\}.$$ Then which of the following is true ?
A
$$f\left( x \right)$$ is differentiable everywhere
B
$$f\left( x \right)$$ is not differentiable at $$x = 0$$
C
$$f\left( x \right) \geqslant 1$$ for all $$x\, \in \,R$$
D
$$f\left( x \right)$$ is not differentiable at $$x = 1$$
Answer :
$$f\left( x \right)$$ is differentiable everywhere
78. Solve this : $$\frac{{{d^n}}}{{d{x^n}}}\left( {\log \,x} \right) = ?$$
A
$$\frac{{\left( {n - 1} \right)!}}{{{x^n}}}$$
B
$$\frac{{n!}}{{{x^n}}}$$
C
$$\frac{{\left( {n - 2} \right)!}}{{{x^n}}}$$
D
$${\left( { - 1} \right)^{n - 1}}\frac{{\left( {n - 1} \right)!}}{{{x^n}}}$$
Answer :
$${\left( { - 1} \right)^{n - 1}}\frac{{\left( {n - 1} \right)!}}{{{x^n}}}$$
79. Let $$f$$ be a function which is continuous and differentiable for all real $$x.$$ If $$f\left( 2 \right) = - 4$$ and $$f'\left( x \right) \geqslant 6$$ for all $$x\, \in \left[ {2,\,4} \right],$$ then :
A
$$f\left( 4 \right) < 8$$
B
$$f\left( 4 \right) \geqslant 8$$
C
$$f\left( 4 \right) \geqslant 12$$
D
none of these
Answer :
$$f\left( 4 \right) \geqslant 8$$
80. Suppose $$f\left( x \right)$$ is differentiable at $$x = 1$$ and $$\mathop {\lim }\limits_{h \to 0} \frac{1}{h}f\left( {1 + h} \right) = 5,$$ then $$f'\left( 1 \right)$$ equals :
A
$$3$$
B
$$4$$
C
$$5$$
D
$$6$$
Answer :
$$5$$