$$\eqalign{ & {\text{Let }}y = {\tan ^{ - 1}}\left[ {\frac{{\sqrt {1 + {x^2}} - 1}}{x}} \right]{\text{ and }}u = {\tan ^{ - 1}}x \cr & {\text{Put }}x = \tan \,\theta \, \Rightarrow \theta = {\tan ^{ - 1}}x \cr & {\text{Then, }}y = {\tan ^{ - 1}}\left[ {\frac{{\sqrt {1 + {{\tan }^2}\theta } - 1}}{{\tan \,\theta }}} \right] \cr & = {\tan ^{ - 1}}\left[ {\frac{{\sqrt {{{\sec }^2}\theta } - 1}}{{\tan \,\theta }}} \right] \cr & = {\tan ^{ - 1}}\left[ {\frac{{\sec \,\theta - 1}}{{\tan \,\theta }}} \right] \cr & = {\tan ^{ - 1}}\left[ {\frac{{\frac{1}{{\cos \,\theta }} - 1}}{{\frac{{\sin \,\theta }}{{\cos \,\theta }}}}} \right] \cr & = {\tan ^{ - 1}}\left[ {\frac{{1 - \cos \,\theta }}{{\sin \,\theta }}} \right] \cr & = {\tan ^{ - 1}}\left[ {\frac{{2\,{{\sin }^2}\frac{\theta }{2}}}{{2\,\sin \frac{\theta }{2}.\cos \frac{\theta }{2}}}} \right] \cr & \left( {\because \,1 - \cos \,\theta = 2\,{{\sin }^2}\frac{\theta }{2}{\text{ and }}\sin \,x = 2\,\sin \frac{x}{2}.\,\cos \frac{x}{2}} \right) \cr & = {\tan ^{ - 1}}\left[ {\tan \frac{\theta }{2}} \right] \cr & \Rightarrow \,y = \frac{\theta }{2} \cr & \Rightarrow y = \frac{{{{\tan }^{ - 1}}x}}{2}\,\,\,\,\,\,\left[ {\because \,\theta = {{\tan }^{ - 1}}x} \right] \cr & \Rightarrow y = \frac{u}{2}\,;\,\,\,\frac{{dy}}{{du}} = \frac{1}{2} \cr} $$

\[\begin{array}{l} {\rm{Derivative\, of\, }}f\left( x \right) = \left\{ \begin{array}{l} \,\,\,\,a{x^2} + b\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < - 1\\ b{x^2} + ax + a\,\,\,x \ge - 1 \end{array} \right.{\rm{ \,is\,}}\\ f'\left( x \right) = \left\{ \begin{array}{l} \,\,\,\,2ax\,\,\,\,\,\,\,\,\,\,\,\,\,x < - 1\\ 2bx + a\,\,\,\,\,x \ge - 1 \end{array} \right. \end{array}\]
If $$f'\left( x \right)$$  is continuous everywhere then it is also continuous at $$x = - 1$$
$$\eqalign{ & {\left. {f'\left( x \right)} \right|_{x = - 1}} = - 2a = - 2b + a \cr & {\text{or, }}3a = 2b.....({\text{i}}) \cr} $$
From the given choice $$a = 2,\,b = 3$$   satisfied this equation.

$$\eqalign{ & f'\left( {\frac{\pi }{4} + 0} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left| {\cos \,2\left( {\frac{\pi }{4} + h} \right)} \right| - \left| {\cos \,2.\frac{\pi }{4}} \right|}}{h} \cr & f'\left( {\frac{\pi }{4} + 0} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\sin \,2h}}{h} \cr & f'\left( {\frac{\pi }{4} + 0} \right) = 2 \cr} $$

Given that,
$$\mathop {\lim }\limits_{x \to 0} \frac{{\left( {\cos \,x - 1} \right)\left( {\cos \,x - {e^x}} \right)}}{{{x^n}}} = $$       finite non zero number
$$\eqalign{ & \mathop { = \lim }\limits_{x \to 0} \frac{{\left( {1 - \cos \,x} \right)\left( {1 + \cos \,x} \right)\left( {{e^x} - \cos \,x} \right)}}{{{x^n}\left( {1 + \cos \,x} \right)}} \cr & = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{{{\sin }^2}\,x}}{{{x^2}}}} \right).\left( {\frac{{{e^x} - \cos \,x}}{{{x^{n - 2}}}}} \right).\left( {\frac{1}{{1 + \cos \,x}}} \right) \cr & = \mathop {\lim }\limits_{x \to 0} {1^2}.\frac{{{e^x} - \cos \,x}}{{{x^{n - 2}}}}.\frac{1}{2} \cr & = \frac{1}{2}\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - \sin \,x}}{{\left( {x - 2} \right){x^{n - 3}}}}\,\,\,\left[ {{\text{using L'Hospital rule}}} \right] \cr} $$
For this limit to be finite, $$n - 3 = 0 \Rightarrow n = 3$$

$$\eqalign{ & \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + x} - 1}}{x} \cr & = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + x} - 1}}{x} \times \frac{{\sqrt {1 + x} + 1}}{{\sqrt {1 + x} + 1}} \cr & = \mathop {\lim }\limits_{x \to 0} \frac{{1 + x - 1}}{{x\left[ {\sqrt {1 + x} + 1} \right]}} \cr & = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt {1 + x} + 1}} \cr & = \frac{1}{{\sqrt {1 + 0} + 1}} \cr & = \frac{1}{2} \cr} $$

\[\begin{array}{l} f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}\\ = \left\{ \begin{array}{l} x\,\,\,\,;\,\,x < - 1\\ {x^3}\,\,;\,\, - 1 \le x \le 0\\ x\,\,\,\,;\,\,0 \le x \le 1\\ {x^3}\,\,;\,\,x \ge 1 \end{array} \right. \end{array}\]
KEY CONCEPT
A continuous function $$f\left( x \right)$$ is not differentiable at $$x= a$$
If graphically it takes a sharp turn at $$x=a.$$
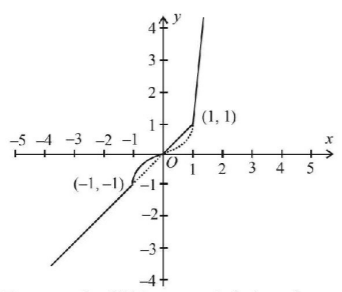
Graph of $$f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}$$     is as shown with solid lines.

From graph of $$f\left( x \right)$$  at $$x =-1, \,0, \,1,$$    we have sharp turns.
$$\therefore f\left( x \right)$$   is not differentiable at $$x =- 1, \,0, \,1.$$

Here $$1 < x < 3$$   and in this interval $${x^2}$$ is an increasing functions, thus $$1 < {x^2} < 9$$
$$\eqalign{ & \left[ {{x^2}} \right] = 1,\,1 \leqslant x < \sqrt 2 \cr & = 2,\,\sqrt 2 \leqslant x < \sqrt 3 \cr & = 3,\,\sqrt 3 \leqslant x < 2 \cr & = 4,\,2 \leqslant x < \sqrt 5 \cr & = 5,\,\sqrt 5 \leqslant x < \sqrt 6 \cr & = 6,\,\sqrt 6 \leqslant x < \sqrt 7 \cr & = 7,\,\sqrt 7 \leqslant x < \sqrt 8 \cr & = 8,\,\sqrt 8 \leqslant x < 3 \cr} $$
Clearly, $$\left[ {{x^2}} \right]$$ and $${a^{\left[ {{x^2}} \right]}}$$ is discontinuous and not differentiable at only $$7$$ points, $$x = \sqrt 2 ,\,\sqrt 3 ,\,2,\,\sqrt 5 ,\,\sqrt 6 ,\,\sqrt 7 ,\,\sqrt 8 $$

$$\eqalign{ & f\left( x \right) = {x^3}\sin \,x \cr & f'\left( x \right) = 3{x^2}\sin \,x + {x^3}\cos \,x \cr & f'\left( x \right) = 0 \cr & \Rightarrow 3{x^2}\sin \,x + {x^3}\cos \,x = 0 \cr & \Rightarrow {x^2}\left( {3\,\sin \,x + x\,\cos \,x} \right) = 0 \cr & \Rightarrow x = 0,\,3\,\sin \,x + x\,\cos \,x = 0.....(1) \cr & {\text{Put }}x = 0,{\text{ in equation }}(1) \cr & 3\,\sin \,x = 0\,\,\, \Rightarrow \sin \,x = 0 \cr & f''\left( x \right) = 6x\,\sin \,x + 3{x^2}\cos \,x + 3{x^2}\cos \,x + {x^3}\left( { - \sin \,x} \right) \cr & f''\left( 0 \right) = 0 \cr} $$

$$\eqalign{ & {\text{For}}\,x \geqslant 0 \cr & \mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} 2 + x = 2 + 1 = 3 \cr & {\text{For}}\,x < 0 \cr & \mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} 2 - x = 2 - 1 = 1 \cr & {\text{So, }}\mathop {\lim }\limits_{x \to 1} f\left( x \right){\text{ does not exist}} \cr & {\text{At }}x = 0 \cr & {\text{R}}{\text{.H}}{\text{.L}}{\text{. :}}\mathop {\lim }\limits_{h \to {0^ + }} f\left( {0 + h} \right) = \mathop {\lim }\limits_{h \to 0} 2 + h = 2 \cr & {\text{L}}{\text{.H}}{\text{.L}}{\text{. :}}\mathop {\lim }\limits_{h \to {0^ - }} f\left( {0 - h} \right) = \mathop {\lim }\limits_{h \to 0} 2 - h = 2 \cr & f\left( 0 \right) = 2 + 0 = 2 \cr & {\text{So, R}}{\text{.H}}{\text{.L}}{\text{.}} = {\text{L}}{\text{.H}}{\text{.L}}{\text{.}} = f\left( 0 \right) \cr & \Rightarrow \,f\left( x \right){\text{ is continuous at}}\,x = 0 \cr & {\text{Differentiability at }}x = 0 \cr & {\text{L}}{\text{.H}}{\text{.D}}{\text{. : }}\mathop {\lim }\limits_{h \to {0^ - }} \frac{{f\left( {0 - h} \right) - f\left( 0 \right)}}{{ - h}} = \mathop {\lim }\limits_{h \to {0^ - }} \frac{{2 + h - 2}}{{ - h}} = \frac{{ - h}}{h} = - 1 \cr & {\text{R}}{\text{.H}}{\text{.D}}{\text{. : }}\mathop {\lim }\limits_{h \to {0^ + }} \frac{{f\left( {0 + h} \right) - f\left( 0 \right)}}{h} = \mathop {\lim }\limits_{h \to {0^ + }} \frac{{2 + h - 2}}{h} = 1 \cr & {\text{Since, L}}{\text{.H}}{\text{.D}}{\text{.}} \ne {\text{R}}{\text{.H}}{\text{.D}}{\text{.}} \cr & {\text{So, }}f\left( x \right){\text{ is not differentiable at }}x = 0. \cr} $$

$$\eqalign{ & {\text{Here, }}u = f\left( {{x^3}} \right) \cr & \Rightarrow \frac{{du}}{{dx}} = f'\left( {{x^3}} \right).\frac{d}{{dx}}\left( {{x^3}} \right) \cr & = \left( {\cos \left( {{x^3}} \right)} \right).3{x^2} \cr & = 3{x^2}.\cos \,{x^3} \cr & {\text{and }}v = g\left( {{x^2}} \right) \cr & \Rightarrow \frac{{dv}}{{dx}} = g'\left( {{x^2}} \right).\frac{d}{{dx}}\left( {{x^2}} \right) \cr & = \left( {\sin \,{x^2}} \right).\left( {2x} \right) \cr & = 2x.\sin \,{x^2} \cr & \therefore \,\frac{{du}}{{dv}} = \frac{{\frac{{du}}{{dx}}}}{{\frac{{dv}}{{dx}}}}\frac{{3{x^2}.\cos \,{x^3}}}{{2x.\sin \,{x^2}}} \cr & \Rightarrow \frac{{du}}{{dv}} = \frac{3}{2}x.\cos \,{x^3}.{\text{cosec}}\,{x^2} \cr} $$