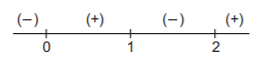31.
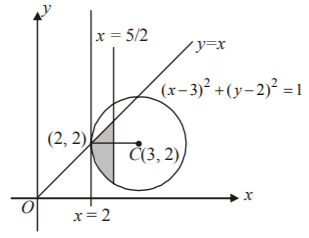
The area of the region formed by $${x^2} + {y^2} - 6x - 4y + 12 \leqslant 0,\,y \leqslant x{\text{ and }}x \leqslant \frac{5}{2}{\text{ is :}}$$ A
$$\left( {\frac{\pi }{6} - \frac{{\sqrt 3 + 1}}{8}} \right){\text{ sq}}{\text{.}}\,{\text{unit}}$$
B
$$\left( {\frac{\pi }{6} + \frac{{\sqrt 3 - 1}}{8}} \right){\text{ sq}}{\text{.}}\,{\text{unit}}$$
C
$$\left( {\frac{\pi }{6} - \frac{{\sqrt 3 - 1}}{8}} \right){\text{ sq}}{\text{.}}\,{\text{unit}}$$
D
None of these
Answer :
$$\left( {\frac{\pi }{6} - \frac{{\sqrt 3 - 1}}{8}} \right){\text{ sq}}{\text{.}}\,{\text{unit}}$$
View Solution
Discuss Question
The required area
$$\eqalign{
& {\text{ = }}\int_2^{\frac{5}{2}} {x\,dx - } \int_2^{\frac{5}{2}} {\left[ {2 - \sqrt {1 - {{\left( {x - 3} \right)}^2}} } \right]dx} \cr
& = \left[ {\frac{{{x^2}}}{2}} \right]_2^{\frac{5}{2}} - \left[ {2x} \right]_2^{\frac{5}{2}} + \left[ {\frac{{x - 3}}{2}\sqrt {1 - {{\left( {x - 3} \right)}^2}} + \frac{1}{2}{{\sin }^{ - 1}}\left( {x - 3} \right)} \right]_2^{\frac{5}{2}} \cr
& = \frac{9}{8} - 1 + \left( { - \frac{{\sqrt 3 }}{8} + \frac{\pi }{6}} \right) \cr
& = \frac{\pi }{6} - \frac{{\sqrt 3 - 1}}{8}{\text{ sq}}{\text{. unit}} \cr} $$
32.
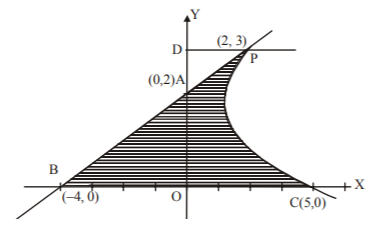
The area of the region bounded by the parabola $${\left( {y - 2} \right)^2} = x - 1,$$ the tangent of the parabola at the point $$\left( {2,\,3} \right)$$ and the $$x$$-axis is : A
6
B
9
C
12
D
3
Answer :
9
View Solution
Discuss Question
The given parabola is $${\left( {y - 2} \right)^2} = x - 1$$
Vertex $$\left( {1,\,2} \right)$$ and it meets $$x$$-axis at $$\left( {5,\,0} \right)$$
Also it gives $${y^2} - 4y - x + 5 = 0$$
So, that equation of tangent to the parabola at $$\left( {2,\,3} \right)$$ is
$$\eqalign{
& y.3 - 2\left( {y + 3} \right) - \frac{1}{2}\left( {x + 2} \right) + 5 = 0 \cr
& {\text{or }}x - 2y + 4 = 0\,\,{\text{which meets }}x{\text{ - axis at }}\left( { - 4,\,0} \right) \cr} $$
In the figure shaded area is the required area.
Let us draw $$PD$$ perpendicular to $$y$$-axis.
Then required area
$$\eqalign{
& = Ar\left( {\Delta BOA} \right) + Ar\left( {OCPD} \right) - Ar\left( {\Delta APD} \right) \cr
& = \frac{1}{2} \times 4 \times 2 + \int_0^3 {x\,dy - \frac{1}{2} \times 2 \times 1} \cr
& = 3 + \int_0^3 {{{\left( {y - 2} \right)}^2} + 1\,dy} \cr
& = 3 + \left[ {\frac{{{{\left( {y - 2} \right)}^3}}}{3} + y} \right]_0^3 \cr
& = 3 + \left[ {\frac{1}{3} + 3 + \frac{8}{3}} \right] \cr
& = 3 + 6 \cr
& = 9\,{\text{sq}}{\text{. units}} \cr} $$
33.
What is the area under the curve $$y = \left| x \right| + \left| {x - 1} \right|$$ between $$x = 0$$ and $$x = 1\,?$$ A
$$\frac{1}{2}$$
B
$$1$$
C
$$\frac{3}{2}$$
D
$$2$$
Answer :
$$1$$
View Solution
Discuss Question
$$\eqalign{
& \left| x \right|\,{\text{for }}x \geqslant 0 \cr
& = x{\text{ and }}\left| {x - 1} \right|{\text{ for }}x \leqslant 1 = - \left( {x - 1} \right), \cr
& {\text{So, }}\int_0^1 {\left( {\left| x \right| + \left| {x - 11} \right|} \right)} = {\text{required area}} \cr
& a = \int_0^1 {x\,dx} - \int_0^1 {\left( {x - 1} \right)dx} \cr
& \,\,\,\,\, = \left[ {\frac{{{x^2}}}{2}} \right]_0^1 - \left[ {\frac{{{x^2}}}{2} - x} \right]_0^1 \cr
& \,\,\,\,\, = \frac{1}{2} - \left( {\frac{1}{2} - 1} \right) \cr
& \,\,\,\,\, = 1{\text{ sq}}{\text{. unit}} \cr} $$
34.
Area of the region $$\left\{ {\left( {x,\,y} \right) \in {{R}^2}\,:\,y \geqslant \sqrt {\left| {x + 3} \right|} ,\,5y \leqslant x + 9 \leqslant 15} \right\}$$ is equal to : A
$$\frac{1}{6}$$
B
$$\frac{4}{3}$$
C
$$\frac{3}{2}$$
D
$$\frac{5}{3}$$
Answer :
$$\frac{3}{2}$$
View Solution
Discuss Question
Area $$ABE$$ (under parabola) $$ = \int_{ - 4}^{ - 3} {\sqrt { - x - 3} dx} = \frac{2}{3}$$
Area $$BCD$$ (under parabola) $$ = \int_{ - 3}^1 {\sqrt {x + 3} dx} = \frac{{16}}{3}$$
Area of trapezium $$ACDE = \frac{1}{2}\left( {1 + 2} \right)5 = \frac{{15}}{2}$$
Required area $$ = \frac{{15}}{2} - \frac{{16}}{3} - \frac{2}{3} = \frac{3}{2}$$
35.
Let $$f\left( x \right)$$ be a function defined by $$f\left( x \right) = \int_1^x {x\left( {{x^2} - 3x + 2} \right)dx,\,1 \leqslant x \leqslant 3.} $$ Then the range of $$f\left( x \right)$$ is : A
$$\left[ {0,\,2} \right]$$
B
$$\left[ { - \frac{1}{4},\,4} \right]$$
C
$$\left[ { - \frac{1}{4},\,2} \right]$$
D
none of these
Answer :
$$\left[ { - \frac{1}{4},\,2} \right]$$
View Solution
Discuss Question
$$\eqalign{
& f'\left( x \right) = x\left( {{x^2} - 3x + 2} \right) = x\left( {x - 1} \right)\left( {x - 2} \right) \cr
& {\text{The sign scheme for}}\,{\text{ }}f'\left( x \right){\text{ is as below}}{\text{.}} \cr} $$
$$\eqalign{
& \therefore f'\left( x \right) \leqslant 0{\text{ in }}1 \leqslant x \leqslant 2{\text{ and }}f'\left( x \right) \geqslant 0{\text{ in }}2 \leqslant x \leqslant 3 \cr
& \therefore f\left( x \right)\,{\text{is m}}{\text{.d}}{\text{. in }}\left[ {1,\,2} \right]{\text{ and m}}{\text{.i}}{\text{. in }}\left[ {2,\,3} \right] \cr
& \therefore \min f\left( x \right) = f\left( 2 \right) = \int_1^2 {x\left( {{x^2} - 3x + 2} \right)dx} \cr
& = \left[ {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right]_1^2 \cr
& = - \frac{1}{4} \cr
& \max f\left( x \right) = {\text{the greatest among}}\left\{ {f\left( 1 \right),\,f\left( 3 \right)} \right\} \cr
& f\left( 1 \right) = \int_1^1 {x\left( {{x^2} - 3x + 2} \right)dx} = 0 \cr
& f\left( 3 \right) = \int_1^3 {x\left( {{x^2} - 3x + 2} \right)dx} = \left[ {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right]_1^3 = 2 \cr
& \therefore \max f\left( x \right) = 2.\,\,{\text{So, the range }} = \left[ { - \frac{1}{4},\,2} \right] \cr} $$
36.
$$\int_0^\pi {{{\sin }^6}x.{{\cos }^5}x\,dx} $$ is equal to : A
$$2\int_0^{\frac{\pi }{2}} {{{\sin }^{50}}x.{{\cos }^{47}}x\,dx} $$
B
$$0$$
C
$$1$$
D
none of these
Answer :
$$0$$
View Solution
Discuss Question
$$\eqalign{
& I = \int_0^\pi {{{\sin }^6}x.{{\cos }^5}x\,dx} = \int_0^\pi {{{\sin }^6}\left( {\pi - x} \right).{{\cos }^5}\left( {\pi - x} \right)\,dx} = - I \cr
& \therefore I = 0 \cr} $$
37.
What is the area enclosed by the equation $${x^2} + {y^2} = 2\,?$$ A
$$4\pi $$ square units
B
$$2\pi $$ square units
C
$$4{\pi ^2}$$ square units
D
$$4$$ square units
Answer :
$$2\pi $$ square units
View Solution
Discuss Question
Given equation of circle is $${x^2} + {y^2} = 2 \Rightarrow y = \sqrt {2 - {x^2}} $$
Required area $$ = 4 \times $$ Area of shaded portion
$$\eqalign{
& = 4\int_0^{\sqrt 2 } {\sqrt {2 - {x^2}} } dx \cr
& = 4\left[ {\frac{x}{2}\sqrt {2 - {x^2}} + \frac{2}{2}{{\sin }^{ - 1}}\frac{x}{{\sqrt 2 }}} \right]_0^{\sqrt 2 } \cr
& = 4\left[ {{{\sin }^{ - 1}}\frac{{\sqrt 2 }}{{\sqrt 2 }}} \right] \cr
& = 4\,{\sin ^{ - 1}}1 \cr
& = 4 \times \frac{\pi }{2} \cr
& = 2\pi {\text{ sq}}{\text{. units}} \cr} $$
38.
The area enclosed between the curve $$y = {\log _e}\left( {x + e} \right)$$ and the coordinate axes is- A
$$1$$
B
$$2$$
C
$$3$$
D
$$4$$
Answer :
$$1$$
View Solution
Discuss Question
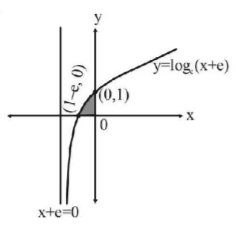
The graph of the curve $$y = {\log _e}\left( {x + e} \right)$$ is as shown in the figure
$$\eqalign{
& {\text{Required area}}\,{\text{:}} \cr
& A = \int\limits_{1 - e}^0 {y\,dx} = \int\limits_{1 - e}^0 {{{\log }_e}\left( {x + e} \right)dx} \cr
& {\text{Put}}\,x + e = t\,\, \Rightarrow dx = dt \cr
& {\text{Also}}\,x = 1 - e,\,\,t = 1 \cr
& {\text{At}}\,x = 0,\,t = e \cr
& \therefore A = \int\limits_1^e {{{\log }_e}t\,dt} = \left[ {t\,{{\log }_e}t - t} \right]_1^e \cr
& e - e - 0 + 1 = 1 \cr} $$
Hence the required area is 1 square unit.
39.
$$\int_0^\pi {\frac{{dx}}{{1 + {3^{\cos \,x}}}}} $$ is equal to : A
$$\pi $$
B
0
C
$$\frac{\pi }{2}$$
D
none of these
Answer :
$$\frac{\pi }{2}$$
View Solution
Discuss Question
$$\eqalign{
& {\text{Let, }}I = \int_0^\pi {\frac{{dx}}{{1 + {3^{\cos \,x}}}}} .....\left( 1 \right) \cr
& {\text{Using above formula,}} \cr
& I = \int_0^\pi {\frac{{dx}}{{1 + {3^{\cos \,\left( {\pi - x} \right)}}}}} = \int_0^\pi {\frac{{{3^{\cos \,x}}dx}}{{1 + {3^{\cos \,x}}}}} ......\left( 2 \right) \cr
& {\text{Adding equation }}\left( 1 \right){\text{ and }}\left( 2 \right){\text{ we get,}} \cr
& I = \frac{1}{2}\int_0^\pi {dx} = \frac{\pi }{2} \cr} $$
40.
$$\int_{ - a}^a {{{\log }_e}\left( {x + \sqrt {1 + {x^2}} } \right)dx} $$ is equal to : A
$$2{\log _e}a$$
B
0
C
$${\log _e}2 + \log \,a$$
D
none of these
Answer :
0
View Solution
Discuss Question
Let $$f\left( x \right) = {\log _e}\left( {x + \sqrt {1 + {x^2}} } \right).$$ Clearly, $$f\left( { - x} \right) = - f\left( { - x} \right).$$