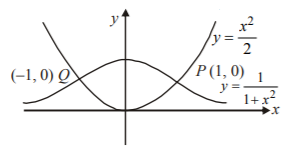11.
Let $$f\left( x \right)$$ be a differentiable function and $$f\left( 1 \right) = 2.$$ If $$\mathop {\lim }\limits_{x \to 1} \int_2^{f\left( x \right)} {\frac{{2t}}{{x - 1}}dt} = 4$$ then the value of $$f'\left( 1 \right)$$ is : A
1
B
2
C
4
D
none of these
Answer :
1
View Solution
Discuss Question
$$\eqalign{
& {\text{Here, }}4 = \mathop {\lim }\limits_{x \to 1} \frac{1}{{x - 1}}\int_2^{f\left( x \right)} {2t\,dt} \cr
& = \mathop {\lim }\limits_{x \to 1} \frac{{2f\left( x \right).f'\left( x \right)}}{1}\,\,\,\left( {{\text{using L'Hospital's}}\,{\text{rule}}} \right) \cr
& \therefore 4 = 2f\left( 1 \right).f'\left( 1 \right) \cr
& \therefore f'\left( 1 \right) = 1 \cr} $$
12.
If $$f\left( x \right) = \int_x^{{x^2}} {\frac{{dt}}{{1 + {t^3}}}} $$ then $$f'\left( 2 \right)$$ is equal to : A
$$\frac{{101}}{{585}}$$
B
$$\frac{{ - 29}}{{585}}$$
C
$$\frac{{ - 56}}{{585}}$$
D
none of these
Answer :
$$\frac{{ - 29}}{{585}}$$
View Solution
Discuss Question
$$\eqalign{
& f\left( x \right) = \int_0^{{x^2}} {\frac{{dt}}{{1 + {t^3}}}} - \int_0^x {\frac{{dt}}{{1 + {t^3}}}} \cr
& \therefore f'\left( x \right) = \frac{d}{{d{x^2}}}\left\{ {\int_0^{{x^2}} {\frac{{dt}}{{1 + {t^3}}}} } \right\}\frac{{d\left( {{x^2}} \right)}}{{dx}} - \frac{1}{{1 + {x^3}}} \cr
& \therefore f'\left( x \right) = \frac{1}{{1 + {x^6}}}.2x - \frac{1}{{1 + {x^3}}} \cr
& \therefore f'\left( 2 \right) = \frac{{2 \times 2}}{{1 + {2^6}}} - \frac{1}{{1 + {2^3}}} = \frac{4}{{65}} - \frac{1}{9} = \frac{{ - 29}}{{585}} \cr} $$
13.
The figure shows as triangle $$AOB$$ and the parabola $$y = {x^2}.$$ The ratio of the area of the triangle $$AOB$$ to the area of the region $$AOB$$ of the parabola $$y = {x^2}$$ is equal to
A
$$\frac{3}{5}$$
B
$$\frac{3}{4}$$
C
$$\frac{7}{8}$$
D
$$\frac{5}{6}$$
Answer :
$$\frac{3}{4}$$
View Solution
Discuss Question
Area of $$\Delta AOB = \frac{1}{2} \times 2a \times {a^2} = {a^3}{\text{units}}$$
Area of region $$AOB = 2\int\limits_0^{{a^2}} {x\,dy} = 2\int\limits_0^{{a^2}} {\sqrt y \,dy} = 2\left[ {\frac{{{y^{\frac{3}{2}}}}}{{\frac{3}{2}}}} \right]_0^{{a^2}} = \frac{4}{3}{a^3}{\text{units}}$$
$$\therefore $$ ratio of areas $$ = \frac{{{a^3}}}{{\frac{4}{3}{a^3}}} = \frac{3}{4}$$
14.
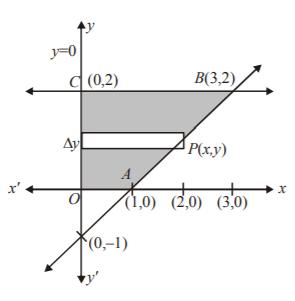
Area bounded by the curves $$y = \left[ {\frac{{{x^2}}}{{64}} + 2} \right]$$
( $$\left[ . \right]$$ denotes the greatest integer function ), $$v = x – 1$$ and $$x = 0,$$ above the $$x$$-axis is : A
2 square units
B
3 square units
C
4 square units
D
None of these
Answer :
4 square units
View Solution
Discuss Question
$$\eqalign{
& {\text{We have, }}0 \leqslant \frac{{{x^2}}}{{64}} < 1,{\text{ if}}\, - 8 < x < 8 \cr
& \Rightarrow 2 \leqslant \frac{{{x^2}}}{{64}} + 2 < 3,{\text{ if }}\,\left| x \right| < 8 \cr
& \Rightarrow y = \left[ {\frac{{{x^2}}}{{64}} + 2} \right] = 2,{\text{ if }}\,\left| x \right| < 8 \cr} $$
The graphs of the given curves is as shown in figure.
$$\eqalign{
& {\text{Required area}} = {\text{area of the shaded region}} \cr
& = \int_0^2 {x\,dy} \cr
& = \int_0^2 {\left( {y + 1} \right)dy} \cr
& = \frac{1}{2}\left[ {\left( {y + 1} \right)} \right]_0^2 \cr
& = \frac{9}{2} - \frac{1}{2} \cr
& = 4{\text{ sq}}{\text{. units}} \cr} $$
15.
$$\int_{\frac{\pi }{5}}^{\frac{{3\pi }}{{10}}} {\frac{{\cos \,x}}{{\cos \,x + \sin \,x}}dx} $$ is equal to : A
$$\pi $$
B
$$\frac{\pi }{2}$$
C
$$\frac{\pi }{4}$$
D
none of these
Answer :
none of these
View Solution
Discuss Question
$$\eqalign{
& {\text{Put }}x = \frac{\pi }{2} - z \cr
& {\text{Then}}\,\,I = \int_{\frac{{3\pi }}{{10}}}^{\frac{\pi }{5}} {\frac{{\cos \left( {\frac{\pi }{2} - z} \right)}}{{\cos \left( {\frac{\pi }{2} - z} \right) + \sin \left( {\frac{\pi }{2} - z} \right)}}} d\left( {\frac{\pi }{2} - z} \right) \cr
& \therefore I = - \int_{\frac{{3\pi }}{{10}}}^{\frac{\pi }{5}} {\frac{{\sin \,z}}{{\sin \,z + \cos \,z}}dz} = \int_{\frac{\pi }{5}}^{\frac{{3\pi }}{{10}}} {\frac{{\sin \,x}}{{\sin \,x + \cos \,x}}dx} \cr
& \therefore I + I = \int_{\frac{\pi }{5}}^{\frac{{3\pi }}{{10}}} {\frac{{\cos \,x}}{{\cos \,x + \sin \,x}}dx} + \int_{\frac{\pi }{5}}^{\frac{{3\pi }}{{10}}} {\frac{{\sin \,x}}{{\sin \,x + \cos \,x}}dx} \cr
& = \int_{\frac{\pi }{5}}^{\frac{{3\pi }}{{10}}} {dx} \cr
& = \frac{{3\pi }}{{10}} - \frac{\pi }{5} \cr
& = \frac{\pi }{{10}} \cr} $$
16.
If $$f\left( x \right)$$ and $$g\left( x \right)$$ be continuous functions over the closed interval $$\left[ {0,\,a} \right]$$ such that $$f\left( x \right) = f\left( {a - x} \right)$$ and $$g\left( x \right) + g\left( {a - x} \right) = 2.$$ Then $$\int_0^a {f\left( x \right).g\left( x \right)dx} $$ is equal to : A
$$\int_0^a {f\left( x \right)dx} $$
B
$$\int_0^a {g\left( x \right)dx} $$
C
$$2a$$
D
none of these
Answer :
$$\int_0^a {f\left( x \right)dx} $$
View Solution
Discuss Question
$$\eqalign{
& \int_0^a {f\left( x \right).g\left( x \right)dx = } \int_0^a {f\left( {a - x} \right).g\left( {a - x} \right)dx} \,\,\,\,\left( {{\text{by property}}} \right) \cr
& = \int_0^a {f\left( x \right).\left\{ {2 - g\left( x \right)} \right\}dx} \,\,\,\,\,\,\left( {{\text{from the question}}} \right) \cr
& = 2\int_0^a {f\left( x \right)dx - } \int_0^a {f\left( x \right).g\left( x \right)dx} \cr
& \therefore \,\,2\int_0^a {f\left( x \right).g\left( x \right)dx} = 2\int_0^a {f\left( x \right)dx} \cr} $$
17.
$$\int_0^a {\left\{ {f\left( x \right) + f\left( { - x} \right)} \right\}dx} $$ is equal to : A
$$2\int_0^a {f\left( x \right)dx} $$
B
$$\int_{ - a}^a {f\left( x \right)dx} $$
C
0
D
$$ - \int_{ - a}^a {f\left( { - x} \right)dx} $$
Answer :
$$\int_{ - a}^a {f\left( x \right)dx} $$
View Solution
Discuss Question
$$\eqalign{
& I = \int_0^a {f\left( x \right)dx} + \int_0^a {f\left( { - x} \right)dx} \cr
& \,\,\,\,\, = \int_0^a {f\left( x \right)dx + } \int_0^{ - a} {f\left( z \right)d\left( { - z} \right)} \cr
& \,\,\,\,\, = \int_0^a {f\left( x \right)dx + } \int_{ - a}^0 {f\left( z \right)dz} \cr
& \,\,\,\,\, = \int_0^a {f\left( x \right)dx} + \int_{ - a}^0 {f\left( x \right)dx} \cr
& \,\,\,\,\, = \int_{ - a}^a {f\left( x \right)dx} \cr} $$
18.
The area enclosed by the curve $$x = a\,{\cos ^3}t,\,y = b\,{\sin ^3}t$$ and the positive directions of $$x$$-axis and $$y$$-axis is : A
$$\frac{{\pi ab}}{4}$$
B
$$\frac{{\pi ab}}{{32}}$$
C
$$\frac{{3\pi ab}}{{32}}$$
D
$$\frac{{5\pi ab}}{{32}}$$
Answer :
$$\frac{{3\pi ab}}{{32}}$$
View Solution
Discuss Question
$$y = 0,$$ when $$t = 0$$ and then $$x = a$$
19.
If $${c_1} = y = \frac{1}{{1 + {x^2}}}$$ and $${c_2} = y = \frac{{{x^2}}}{2}$$ be two curves lying in $$XY$$ -plane, then : A
area bounded by curve $$y = \frac{1}{{1 + {x^2}}}$$ and $$y = 0$$ is $$\frac{\pi }{2}$$
B
area bounded by $${c_1}$$ and $${c_2}$$ is $$\frac{\pi }{2} - 1$$
C
area bounded by $${c_1}$$ and $${c_2}$$ is $$1 - \frac{\pi }{2}$$
D
area bounded by curve $$y = \frac{1}{{1 + {x^2}}}$$ and $$x$$-axis is $$\frac{\pi }{2}$$
Answer :
area bounded by $${c_1}$$ and $${c_2}$$ is $$\frac{\pi }{2} - 1$$
View Solution
Discuss Question
Area bounded by $$y = \frac{1}{{1 + {x^2}}}$$ and $$x$$-axis is $$\int_{ - \infty }^\infty {\frac{1}{{1 + {x^2}}}} dx = \pi $$
Area bounded by two curves is $$ = \int_{ - 1}^1 {\left( {\frac{1}{{1 + {x^2}}} - \frac{{{x^2}}}{2}} \right)} dx = \frac{\pi }{2} - 1$$
20.
What is the area bounded by $$y = \tan \,x,\,y = 0$$ and $$x = \frac{\pi }{4}\,?$$ A
$$\ln\,2$$ square units
B
$$\frac{{\ln\,2}}{2}$$ square units
C
$$2\left( {\ln} \right)2$$ square units
D
None of these
Answer :
$$\frac{{\ln\,2}}{2}$$ square units
View Solution
Discuss Question
Required area