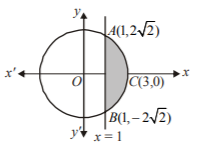151. Let $$f\left( x \right)$$ be a continuous function such that the area bounded by the curve $$y = f\left( x \right),$$ the $$x$$-axis and the two ordinates $$x=0$$ and $$x=a$$ is $$\frac{{{a^2}}}{2} + \frac{a}{2}\sin \,a + \frac{\pi }{2}\cos \,a.$$ Then $$f\left( {\frac{\pi }{2}} \right)$$ is :
A
$$\frac{1}{2}$$
B
$$\frac{{{\pi ^2}}}{8} + \frac{\pi }{4}$$
C
$$\frac{{\pi + 1}}{2}$$
D
$$\frac{\pi }{2}$$
Answer :
$$\frac{1}{2}$$
152. The area of the smaller segment cut off from the circle $${x^2} + {y^2} = 9$$ by $$x = 1$$ is :
A
$$\frac{1}{2}\left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}}$$
B
$$\left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}}$$
C
$$\left( {\sqrt 8 - 9\,{{\sec }^{ - 1}}3} \right){\text{sq}}{\text{.unit}}$$
D
None of the above
Answer :
$$\left( {9\,{{\sec }^{ - 1}}3 - \sqrt 8 } \right){\text{sq}}{\text{.unit}}$$
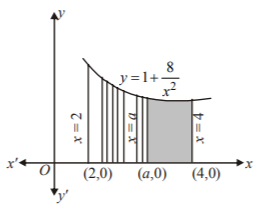
153. If the ordinate $$x = a$$ divides the area bounded by $$x$$-axis, part of the curve $$y = 1 + \frac{8}{{{x^2}}}$$ and the ordinates $$x = 2,\,x = 4$$ into two equal parts, then $$a$$ is equal to :
A
$$\sqrt 2 $$
B
$$2\sqrt 2 $$
C
$$3\sqrt 2 $$
D
None of these
Answer :
$$2\sqrt 2 $$
154. The area of the region enclosed by the curves $$y = x,\,x = e,\,y = \frac{1}{x}$$ and the positive $$x$$-axis is
A
$$1$$ square unit
B
$$\frac{3}{2}$$ square unit
C
$$\frac{5}{2}$$ square unit
D
$$\frac{1}{2}$$ square unit
Answer :
$$\frac{3}{2}$$ square unit
155. Let $$f\left( x \right)$$ be a continuous function such that the area bounded by the curve $$y = f\left( x \right),\,x$$ -axis and the lines $$x = 0$$ and $$x = a$$ is $$\frac{{{a^2}}}{2} + \frac{a}{2}\sin \,a + \frac{\pi }{2}\cos \,a,$$ then $$f\left( {\frac{\pi }{2}} \right) = ?$$
A
$$1$$
B
$$\frac{1}{2}$$
C
$$\frac{1}{3}$$
D
None of these
Answer :
$$\frac{1}{2}$$
156. Area bounded by the curves $$y = {e^x},\,y = {e^{ - x}}$$ and the straight line $$x = 1$$ is (in sq. units)
A
$$e + \frac{1}{e}$$
B
$$e + \frac{1}{e} + 2$$
C
$$e + \frac{1}{e} - 2$$
D
$$e - \frac{1}{e} + 2$$
Answer :
$$e + \frac{1}{e} - 2$$