51.
If the function $$y = \frac{{ax + b}}{{\left( {x - 1} \right)\left( {x - 4} \right)}}$$ has turning point at $$P\left( {2,\, - 1} \right),$$ then : A
$$a = b = 1$$
B
$$a = b = 0$$
C
$$a = 1,\,b = 0$$
D
$$a = b = 2$$
Answer :
$$a = 1,\,b = 0$$
View Solution
Discuss Question
$$y = \frac{{ax + b}}{{\left( {x - 1} \right)\left( {x - 4} \right)}} = \frac{{ax + b}}{{{x^2} - 5x + 4}}$$ has turning
point at $$P\left( {2,\, - 1} \right).$$
52.
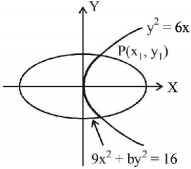
If the curves $${y^2} = 6x,\,9{x^2} + b{y^2} = 16$$ intersect each other at right angles, then the value of $$b$$ is : A
$$\frac{7}{2}$$
B
4
C
$$\frac{9}{2}$$
D
6
Answer :
$$\frac{9}{2}$$
View Solution
Discuss Question
Let curve intersect each other at point $$P\left( {{x_1},{y_1}} \right)$$
Since, point of intersection is on both the curves, then
$$y_1^2 = 6{x_1}\,......\left( {\text{i}} \right)\,\,\,\,\,{\text{and}}\,9x_1^2 + by_1^2 = 16\,......\left( {{\text{ii}}} \right)$$
Now, find the slope of tangent to both the curves at the point of intersection $$P\left( {{x_1},{y_1}} \right)$$
For slope of curves:
curve (i):
$${\left( {\frac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = {m_1} = \frac{3}{{{y_1}}}$$
curve (ii):
$${\text{and}}\,{\left( {\frac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = {m_2} = - \frac{{9{x_1}}}{{b{y_1}}}$$
Since, both the curves intersect each other at right angle then,
$$\eqalign{
& {m_1}{m_2} = - 1 \Rightarrow \frac{{27{x_1}}}{{by_{_1}^2}} = 1 \Rightarrow b = 27\frac{{{x_1}}}{{y_{_1}^2}} \cr
& \therefore \,\,{\text{from}}\,{\text{equation}}\,\left( {\text{i}} \right),\,b = 27 \times \frac{1}{6} = \frac{9}{2} \cr} $$
53.
The tangent to the curve $$y = {e^x}$$ drawn at the point $$\left( {c,{e^e}} \right)$$ intersects the line joining the points $$\left( {c - 1,{e^{c - 1}}} \right)$$ and $$\left( {c + 1,{e^{c + 1}}} \right)$$ A
on the left of $$x = c$$
B
on the right $$x = c$$
C
at no point
D
at all points
Answer :
on the left of $$x = c$$
View Solution
Discuss Question
$$\eqalign{
& {\text{The equation of tangent to the curve}}\,y = {e^x}\,{\text{at}}\,\left( {c,{e^c}} \right)\,{\text{is}} \cr
& y - {e^c} = {e^c}\left( {x - c} \right)\,\,......\left( 1 \right) \cr
& {\text{and equation of line joining}}\,\left( {c - 1,{e^{c - 1}}} \right)\,{\text{and}}\,\left( {c + 1,{e^{c + 1}}} \right)\,{\text{is}} \cr
& y - {e^{c - 1}} = \frac{{{e^{c + 1}} - {e^{c - 1}}}}{{\left( {c + 1} \right) - \left( {c - 1} \right)}}\left[ {x - \left( {c - 1} \right)} \right] \cr
& \Rightarrow y - {e^{c - 1}} = \frac{{{e^c}\left( {e - {e^{ - 1}}} \right)}}{2}\left[ {x - c + 1} \right]\,\,......\left( 2 \right) \cr
& {\text{Subtracting equation }}\left( {\text{1}} \right){\text{ from }}\left( {\text{2}} \right){\text{, we get}} \cr
& {e^c} - {e^{c - 1}} = {e^c}\left( {x - c} \right)\left[ {\frac{{e - {e^{ - 1}} - 2}}{2}} \right] + {e^c}\left( {\frac{{e - {e^{ - 1}}}}{2}} \right) \cr
& \Rightarrow x - c = \frac{{\left[ {1 - {e^{ - 1}} - \left( {\frac{{e - {e^{ - 1}}}}{2}} \right)} \right]}}{{\frac{{e - {e^{ - 1}} - 2}}{2}}} = \frac{{2 - e - {e^{ - 1}}}}{{e - {e^{ - 1}} - 2}} \cr
& = \frac{{e + {e^{ - 1}} - 2}}{{2 - \left( {e - {e^{ - 1}}} \right)}} = \frac{{\frac{{e + {e^{ - 1}}}}{2} - 1}}{{1 - \frac{{e - {e^{ - 1}}}}{2}}} = \frac{{ + ve}}{{ - ve}} = - ve \cr
& \Rightarrow x - c < 0 \Rightarrow x < c \cr
& \therefore {\text{The two lines meet on the left of line}}\,x = c \cr} $$
54.
Let the function $$f\left( x \right)$$ be defined as below. A
1
B
$$-1$$
C
0
D
none of these
Answer :
none of these
View Solution
Discuss Question
$$\eqalign{
& \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {1 + h} \right) - f\left( 1 \right)}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{2\left( {1 + h} \right) - 2}}{h} = \mathop {\lim }\limits_{h \to 0} 2 = 2 \cr
& \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {1 - h} \right) - f\left( 1 \right)}}{{ - h}} = \mathop {\lim }\limits_{h \to 0} \frac{{{{\sin }^{ - 1}}\lambda + {{\left( {1 - h} \right)}^2} - 2}}{{ - h}} \cr
& = \mathop {\lim }\limits_{h \to 0} \frac{{{{\sin }^{ - 1}}\lambda - 1 - 2h + {h^2}}}{{ - h}} = 2{\text{ if }}{\sin ^{ - 1}}\lambda = 1,\,{\text{i}}{\text{.e}}{\text{.,}}\,\lambda = \sin \,1 \cr
& \therefore \,f\left( x \right)\,{\text{is differentiable at }}x = 1\,\,{\text{if }}\lambda = {\text{sin}}\,{\text{1}}.{\text{ Then}} \cr
& f'\left( x \right) = 2x,\,0 < x < 1{\text{ and }}f'\left( x \right) = 2,\,x \geqslant 1 \cr
& \therefore f'\left( {1 - \in } \right) = 2\left( {1 - \in } \right) > 0{\text{ and }}f'\left( {1 + \in } \right) = 2 > 0 \cr} $$
55.
Let $$f\left( x \right) = {x^3} - 6{x^2} + 12x - 3.$$ Then at $$x = 2,\,f\left( x \right)$$ has : A
a maximum
B
a minimum
C
both a maximum and a minimum
D
neither a maximum nor a minimum
Answer :
neither a maximum nor a minimum
View Solution
Discuss Question
$$\eqalign{
& f'\left( x \right) = 3{x^2} - 12x + 12 = 3{\left( {x - 2} \right)^2} \cr
& \therefore \,f'\left( 2 \right) = 0\,; \cr
& f'\left( {2 - \in } \right) = 3{ \in ^2} > 0\,; \cr
& f'\left( {2 + \in } \right) = 3{ \in ^2} > 0 \cr} $$
56.
What is the product of two parts of 20, such that the product of one part and the cube of the other is maximum ? A
75
B
91
C
84
D
96
Answer :
75
View Solution
Discuss Question
Let 20 be divided in two parts such that first part $$ = x$$
57.
If $$f\left( x \right) = x\,\ell n\,x,$$ then $$f\left( x \right)$$ attains minimum value at which one of the following points ? A
$$x = {e^{ - 2}}$$
B
$$x = e$$
C
$$x = {e^{ - 1}}$$
D
$$x = 2{e^{ - 1}}$$
Answer :
$$x = {e^{ - 1}}$$
View Solution
Discuss Question
$$\eqalign{
& {\text{Let }}f\left( x \right) = x\,\ln \,x \cr
& f'\left( x \right) = \frac{x}{x} + \ln \,x = 1 + \ln \,x \cr
& {\text{Put }}f'\left( x \right) = 0 \Rightarrow 1 + \ln \,x \cr
& \Rightarrow \ln \,x = - 1 \Rightarrow x = {e^{ - 1}} \cr
& {\text{Now, }}f''\left( x \right) = \frac{1}{x} \cr
& {\left. {f''\left( x \right)} \right|_{x = {e^{ - 1}}}} = \frac{1}{{{e^{ - 1}}}} = e > 0 \cr} $$
58.
If $$q$$ denotes the acute angle between the curves, $$y = 10 - {x^2}$$ and $$y = 2 + {x^2}$$ at a point of their intersection, then $$\left| {\tan \theta } \right|$$ is equal to: A
$$\frac{4}{9}$$
B
$$\frac{8}{{15}}$$
C
$$\frac{7}{{17}}$$
D
$$\frac{8}{{17}}$$
Answer :
$$\frac{8}{{15}}$$
View Solution
Discuss Question
Since, the equation of curves are
59.
Consider the two curves $${C_1}:{y^2} = 4x,\,{C_2}:{x^2} + {y^2} - 6x + 1 = 0.$$ Then, A
$${C_1}\,{\text{and}}\,{C_2}$$ touch each other only at one point.
B
$${C_1}\,{\text{and}}\,{C_2}$$ touch each other exactly at two points
C
$${C_1}\,{\text{and}}\,{C_2}$$ intersect (but do not touch) at exactly two points
D
$${C_1}\,{\text{and}}\,{C_2}$$ neither intersect nor touch each other
Answer :
$${C_1}\,{\text{and}}\,{C_2}$$ touch each other exactly at two points
View Solution
Discuss Question
The given curves are
60.
If the sub-normal at any point on $$y = {a^{1 - n}}{x^n}$$ is of constant length, then the value of $$n$$ is : A
$$\frac{1}{4}$$
B
$$1$$
C
$$\frac{1}{3}$$
D
$$\frac{1}{2}$$
Answer :
$$\frac{1}{2}$$
View Solution
Discuss Question
$$\eqalign{
& y = {a^{1 - n}}{x^n}{\text{ or }}\frac{{dy}}{{dx}} = {a^{1 - n}}n{x^{n - 1}} \cr
& {\text{Sub - normal}} = \left| {y\frac{{dy}}{{dx}}} \right| \cr
& = \left| {y{a^{1 - n}}n{x^{n - 1}}} \right| \cr
& = \left| {{a^{1 - n}}{x^n}{a^{1 - n}}n{x^{n - 1}}} \right| \cr
& = \left| {{a^{2 - 2n}}{x^{2n - 1}}} \right| \cr
& {\text{which is constant if }}2n - 1 = 0{\text{ or }}n = \frac{1}{2} \cr} $$