Question
Let $$PS$$ be the median of the triangle with vertices $$P\left( {2,\,2} \right),\,Q\left( {6,\, - 1} \right)$$ and $$R\left( {7,\,3} \right).$$ The equation of the line passing through $$\left( {1,\, - 1} \right)$$ and parallel to $$PS$$ is-
A.
$$2x-9y-7=0$$
B.
$$2x-9y-11=0$$
C.
$$2x+9y-11=0$$
D.
$$2x+9y+7=0$$
Answer :
$$2x+9y+7=0$$
Solution :
$$S$$ is the midpoint of $$Q$$ and $$R$$
Therefore, $$S \equiv \left( {\frac{{7 + 6}}{2},\,\frac{{3 - 1}}{2}} \right) = \left( {\frac{{13}}{2},\,1} \right)$$
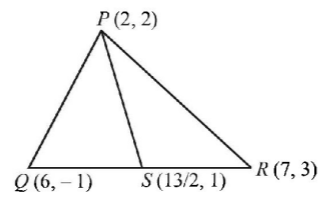
Now slope of $$PS = m = \frac{{2 - 1}}{{2 - \frac{{13}}{2}}} = - \frac{2}{9}$$
Now equation of the line passing through $$\left( {1,\, - 1} \right)$$ and parallel to $$PS$$ is
$$y + 1 = - \frac{2}{9}\left( {x - 1} \right)\,\,\,{\text{or}}\,\,\,2x + 9y + 7 = 0$$
$$S$$ is the midpoint of $$Q$$ and $$R$$
Therefore, $$S \equiv \left( {\frac{{7 + 6}}{2},\,\frac{{3 - 1}}{2}} \right) = \left( {\frac{{13}}{2},\,1} \right)$$

Now slope of $$PS = m = \frac{{2 - 1}}{{2 - \frac{{13}}{2}}} = - \frac{2}{9}$$
Now equation of the line passing through $$\left( {1,\, - 1} \right)$$ and parallel to $$PS$$ is
$$y + 1 = - \frac{2}{9}\left( {x - 1} \right)\,\,\,{\text{or}}\,\,\,2x + 9y + 7 = 0$$