Question
Let $$P$$ be the point on the parabola, $${y^2} = 8x$$ which is at a minimum distance from the centre $$C$$ of the circle, $${x^2} + {\left( {y + 6} \right)^2} = 1.$$ Then the equation of the circle, passing through $$C$$ and having its centre at $$P$$ is:
A.
$${x^2} + {y^2} - \frac{x}{4} + 2y - 24 = 0$$
B.
$${x^2} + {y^2} - 4x + 9y + 18 = 0$$
C.
$${x^2} + {y^2} - 4x + 8y + 12 = 0$$
D.
$${x^2} + {y^2} - x + 4y - 12 = 0$$
Answer :
$${x^2} + {y^2} - 4x + 8y + 12 = 0$$
Solution :
Minimum distance $$ \Rightarrow $$ perpendicular distance
Equation of normal at $$p\left( {2{t^2},\,4t} \right)$$
$$y = - tx + 4t + 2{t^3}$$
It passes through $$C\left( {0,\, - 6} \right)\,\, \Rightarrow {t^3} + 2t + 3 = 0\,\, \Rightarrow t = - 1$$
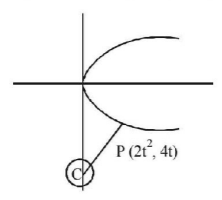
Centre of new circle $$ = P\left( {2{t^2},\,4t} \right) = P\left( {2,\, - 4} \right)$$
Radius $$ = PC = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( { - 4 + 6} \right)}^2}} = 2\sqrt 2 $$
$$\therefore $$ Equation of the circle is
$$\eqalign{ & {\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = {\left( {2\sqrt 2 } \right)^2} \cr & \Rightarrow {x^2} + {y^2} - 4x + 8y + 12 = 0 \cr} $$
Minimum distance $$ \Rightarrow $$ perpendicular distance
Equation of normal at $$p\left( {2{t^2},\,4t} \right)$$
$$y = - tx + 4t + 2{t^3}$$
It passes through $$C\left( {0,\, - 6} \right)\,\, \Rightarrow {t^3} + 2t + 3 = 0\,\, \Rightarrow t = - 1$$

Centre of new circle $$ = P\left( {2{t^2},\,4t} \right) = P\left( {2,\, - 4} \right)$$
Radius $$ = PC = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( { - 4 + 6} \right)}^2}} = 2\sqrt 2 $$
$$\therefore $$ Equation of the circle is
$$\eqalign{ & {\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = {\left( {2\sqrt 2 } \right)^2} \cr & \Rightarrow {x^2} + {y^2} - 4x + 8y + 12 = 0 \cr} $$