Question
Let $$P = \,\left( { - 1,\,0} \right),\,Q = \left( {0,\,0} \right)$$ and $$R = \left( {3,\,3\sqrt 3 } \right)$$ be three point. The equation of the bisector of the angle $$PQR$$ is-
A.
$$\frac{{\sqrt 3 }}{2}x + y = 0$$
B.
$$x + \sqrt {3y} = 0$$
C.
$$\sqrt 3 x + y = 0$$
D.
$$x + \frac{{\sqrt 3 }}{2}y = 0$$
Answer :
$$\sqrt 3 x + y = 0$$
Solution :
Given : The coordinates of points $$P, \,Q, \,R$$ are $$\left( { - 1,\,0} \right),\,\left( {0,\,0} \right),\,\left( {3,\,3\sqrt 3 } \right)$$ respectively.
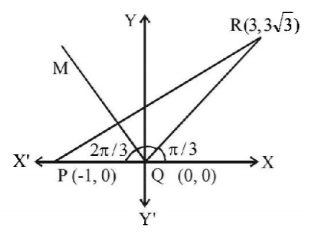
$$\eqalign{ & {\text{Slope of }}QR = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{{3\sqrt 3 }}{3} \cr & \Rightarrow \tan \,\theta = \sqrt 3 \cr & \Rightarrow \theta = \frac{\pi }{3} \cr & \Rightarrow \angle RQX = \frac{\pi }{3} \cr & \therefore \angle RQP = \pi - \frac{\pi }{3} = \frac{{2\pi }}{3} \cr} $$
Let $$QM$$ bisects the $$\angle PQR,$$
$$\therefore $$ Slope of the line $$QM = \tan \frac{{2\pi }}{3} = - \sqrt 3 $$
$$\therefore $$ Equation of line $$QM$$ is $$\left( {y - 0} \right) = - \sqrt 3 \left( {x - 0} \right)$$
$$\eqalign{ & \Rightarrow y = - \sqrt 3 x\,\, \cr & \Rightarrow \sqrt 3 \,x + y = 0 \cr} $$
Given : The coordinates of points $$P, \,Q, \,R$$ are $$\left( { - 1,\,0} \right),\,\left( {0,\,0} \right),\,\left( {3,\,3\sqrt 3 } \right)$$ respectively.

$$\eqalign{ & {\text{Slope of }}QR = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{{3\sqrt 3 }}{3} \cr & \Rightarrow \tan \,\theta = \sqrt 3 \cr & \Rightarrow \theta = \frac{\pi }{3} \cr & \Rightarrow \angle RQX = \frac{\pi }{3} \cr & \therefore \angle RQP = \pi - \frac{\pi }{3} = \frac{{2\pi }}{3} \cr} $$
Let $$QM$$ bisects the $$\angle PQR,$$
$$\therefore $$ Slope of the line $$QM = \tan \frac{{2\pi }}{3} = - \sqrt 3 $$
$$\therefore $$ Equation of line $$QM$$ is $$\left( {y - 0} \right) = - \sqrt 3 \left( {x - 0} \right)$$
$$\eqalign{ & \Rightarrow y = - \sqrt 3 x\,\, \cr & \Rightarrow \sqrt 3 \,x + y = 0 \cr} $$