Question
Let $$P = \left( {1,\,1} \right)$$ and $$Q = \left( {3,\,2} \right).$$ The point $$R$$ on the $$x$$-axis such that $$PR+RQ$$ is the minimum is :
A.
$$\left( {\frac{5}{3},\,0} \right)$$
B.
$$\left( {\frac{1}{3},\,0} \right)$$
C.
$$\left( {3,\,0} \right)$$
D.
none of these
Answer :
$$\left( {\frac{5}{3},\,0} \right)$$
Solution :
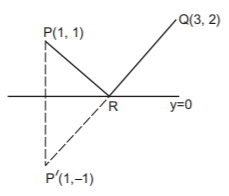
The point $$R$$ should be such that $$PR$$ is reflected along $$RQ$$ from the line $$y=0.$$
The equation of $$P'Q$$ ( where $$P'$$ is the image of $$P$$ ) is $$3x-2y=5.$$
$$R$$ is the point of intersection of $$y=0$$ and $$3x-2y=5.$$

The point $$R$$ should be such that $$PR$$ is reflected along $$RQ$$ from the line $$y=0.$$
The equation of $$P'Q$$ ( where $$P'$$ is the image of $$P$$ ) is $$3x-2y=5.$$
$$R$$ is the point of intersection of $$y=0$$ and $$3x-2y=5.$$