Question
Let $$OP \cdot OQ = 1$$ and let $$O, P, Q$$ be three collinear points. If $$O$$ and $$Q$$ represent the complex numbers $$0$$ and $$z$$ then $$P$$ represents
A.
$$\frac{1}{z}$$
B.
$${\overline z }$$
C.
$$\frac{1}{{\overline z }}$$
D.
None of these
Answer :
$$\frac{1}{{\overline z }}$$
Solution :
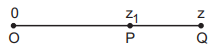
$$\eqalign{ & {\text{Here, }}\left| {0 - {z_1}} \right|\left| {0 - z} \right| = 1. \cr & \therefore \,\,\left| {{z_1}} \right|\left| z \right| = 1 \cr & \therefore \,\,\left| {{z_1}} \right| = \frac{1}{{\left| z \right|}}. \cr & {\text{Also, amp}}\frac{{{z_1} - 0}}{{z - 0}} = 0\,\,\,\,\,\therefore \,\,{\text{amp}}\frac{{{z_1}}}{z} = 0\,\,\,\,\therefore \,\,{\text{amp}}\,{z_1} = {\text{amp }}z. \cr & \therefore \,\,{z_1} = \frac{1}{{\left| z \right|}}\left\{ {\cos \left( {{\text{amp }}{z_1}} \right) + i\sin \left( {{\text{amp }}{z_1}} \right)} \right\} \cr & {z_1} = \frac{1}{{{{\left| z \right|}^2}}} \cdot \left| z \right|\left\{ {\cos \left( {{\text{amp }}z} \right) + i\sin \left( {{\text{amp }}z} \right)} \right\} \cr & {z_1} = \frac{1}{{{{\left| z \right|}^2}}} \cdot z = \frac{z}{{z\overline z }} = \frac{1}{{\overline z }}. \cr} $$

$$\eqalign{ & {\text{Here, }}\left| {0 - {z_1}} \right|\left| {0 - z} \right| = 1. \cr & \therefore \,\,\left| {{z_1}} \right|\left| z \right| = 1 \cr & \therefore \,\,\left| {{z_1}} \right| = \frac{1}{{\left| z \right|}}. \cr & {\text{Also, amp}}\frac{{{z_1} - 0}}{{z - 0}} = 0\,\,\,\,\,\therefore \,\,{\text{amp}}\frac{{{z_1}}}{z} = 0\,\,\,\,\therefore \,\,{\text{amp}}\,{z_1} = {\text{amp }}z. \cr & \therefore \,\,{z_1} = \frac{1}{{\left| z \right|}}\left\{ {\cos \left( {{\text{amp }}{z_1}} \right) + i\sin \left( {{\text{amp }}{z_1}} \right)} \right\} \cr & {z_1} = \frac{1}{{{{\left| z \right|}^2}}} \cdot \left| z \right|\left\{ {\cos \left( {{\text{amp }}z} \right) + i\sin \left( {{\text{amp }}z} \right)} \right\} \cr & {z_1} = \frac{1}{{{{\left| z \right|}^2}}} \cdot z = \frac{z}{{z\overline z }} = \frac{1}{{\overline z }}. \cr} $$