Question
Let $$k$$ be an integer such that triangle with vertices $$(k, -3k), (5, k)$$ and $$(- k, 2)$$ has area $$28\,sq.$$ units. Then the orthocentre of this triangle is at the point:
A.
$$\left( {2,\frac{1}{2}} \right)$$
B.
$$\left( {2, - \frac{1}{2}} \right)$$
C.
$$\left( {1,\frac{3}{4}} \right)$$
D.
$$\left( {1, - \frac{3}{4}} \right)$$
Answer :
$$\left( {2,\frac{1}{2}} \right)$$
Solution :
We have
\[\frac{1}{2}\left| {\left| \begin{array}{l} \,\,k\,\,\,\,\, - 3k\,\,\,\,\,\,\,1\\ \,\,5\,\,\,\,\,\,\,\,\,\,\,k\,\,\,\,\,\,\,\,1\\ - k\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,1 \end{array} \right|} \right| = 28\]
$$\eqalign{ & \Rightarrow \,\,5{k^2} + 13k - 46 = 0 \cr & {\text{or }}5{k^2} + 13k + 66 = 0 \cr & {\text{Now,}}\,\,5{k^2} + 13k - 46 = 0 \cr} $$
$$\eqalign{ & k = \frac{{ - 13 \pm \sqrt {1089} }}{{10}} \cr & \therefore \,\,k = \frac{{ - 23}}{5};\,k = 2 \cr} $$
since $$k$$ is an integer, $$\therefore \,\,k = 2$$
Also $$5{k^2} + 13k + 66 = 0$$
$$ \Rightarrow \,\,k = \frac{{ - 13 \pm \sqrt { - 1151} }}{{10}}$$
So no real solution exist
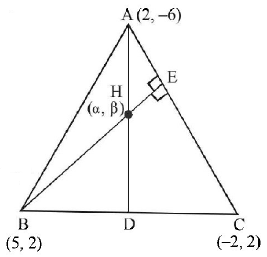
For orthocentre
$$BH \bot AC$$
$$\eqalign{ & \therefore \,\,\left( {\frac{{\beta - 2}}{{\alpha - 5}}} \right)\left( {\frac{8}{{ - 4}}} \right) = - 1 \cr & \Rightarrow \,\,\alpha - 2\beta = 1\,\,\,\,.....\left( 1 \right) \cr} $$
Also $$CH \bot AB$$
$$\eqalign{ & \therefore \,\,\left( {\frac{{\beta - 2}}{{\alpha + 2}}} \right)\left( {\frac{8}{3}} \right) = - 1 \cr & \Rightarrow \,\,3\alpha + 8\beta = 10\,\,\,\,\,.....\left( 2 \right) \cr} $$
Solving (1) and (2), we get
$$\alpha = 2,\beta = \frac{1}{2}$$
orthocentre is $$\left( {2,\frac{1}{2}} \right)$$
We have
\[\frac{1}{2}\left| {\left| \begin{array}{l} \,\,k\,\,\,\,\, - 3k\,\,\,\,\,\,\,1\\ \,\,5\,\,\,\,\,\,\,\,\,\,\,k\,\,\,\,\,\,\,\,1\\ - k\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,1 \end{array} \right|} \right| = 28\]
$$\eqalign{ & \Rightarrow \,\,5{k^2} + 13k - 46 = 0 \cr & {\text{or }}5{k^2} + 13k + 66 = 0 \cr & {\text{Now,}}\,\,5{k^2} + 13k - 46 = 0 \cr} $$

$$\eqalign{ & k = \frac{{ - 13 \pm \sqrt {1089} }}{{10}} \cr & \therefore \,\,k = \frac{{ - 23}}{5};\,k = 2 \cr} $$
since $$k$$ is an integer, $$\therefore \,\,k = 2$$
Also $$5{k^2} + 13k + 66 = 0$$
$$ \Rightarrow \,\,k = \frac{{ - 13 \pm \sqrt { - 1151} }}{{10}}$$
So no real solution exist
For orthocentre
$$BH \bot AC$$
$$\eqalign{ & \therefore \,\,\left( {\frac{{\beta - 2}}{{\alpha - 5}}} \right)\left( {\frac{8}{{ - 4}}} \right) = - 1 \cr & \Rightarrow \,\,\alpha - 2\beta = 1\,\,\,\,.....\left( 1 \right) \cr} $$
Also $$CH \bot AB$$
$$\eqalign{ & \therefore \,\,\left( {\frac{{\beta - 2}}{{\alpha + 2}}} \right)\left( {\frac{8}{3}} \right) = - 1 \cr & \Rightarrow \,\,3\alpha + 8\beta = 10\,\,\,\,\,.....\left( 2 \right) \cr} $$
Solving (1) and (2), we get
$$\alpha = 2,\beta = \frac{1}{2}$$
orthocentre is $$\left( {2,\frac{1}{2}} \right)$$