Question
Let $$f\left( x \right)$$ be a function defined by $$f\left( x \right) = \int_1^x {x\left( {{x^2} - 3x + 2} \right)dx,\,1 \leqslant x \leqslant 3.} $$ Then the range of $$f\left( x \right)$$ is :
A.
$$\left[ {0,\,2} \right]$$
B.
$$\left[ { - \frac{1}{4},\,4} \right]$$
C.
$$\left[ { - \frac{1}{4},\,2} \right]$$
D.
none of these
Answer :
$$\left[ { - \frac{1}{4},\,2} \right]$$
Solution :
$$\eqalign{ & f'\left( x \right) = x\left( {{x^2} - 3x + 2} \right) = x\left( {x - 1} \right)\left( {x - 2} \right) \cr & {\text{The sign scheme for}}\,{\text{ }}f'\left( x \right){\text{ is as below}}{\text{.}} \cr} $$
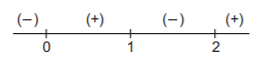
$$\eqalign{ & \therefore f'\left( x \right) \leqslant 0{\text{ in }}1 \leqslant x \leqslant 2{\text{ and }}f'\left( x \right) \geqslant 0{\text{ in }}2 \leqslant x \leqslant 3 \cr & \therefore f\left( x \right)\,{\text{is m}}{\text{.d}}{\text{. in }}\left[ {1,\,2} \right]{\text{ and m}}{\text{.i}}{\text{. in }}\left[ {2,\,3} \right] \cr & \therefore \min f\left( x \right) = f\left( 2 \right) = \int_1^2 {x\left( {{x^2} - 3x + 2} \right)dx} \cr & = \left[ {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right]_1^2 \cr & = - \frac{1}{4} \cr & \max f\left( x \right) = {\text{the greatest among}}\left\{ {f\left( 1 \right),\,f\left( 3 \right)} \right\} \cr & f\left( 1 \right) = \int_1^1 {x\left( {{x^2} - 3x + 2} \right)dx} = 0 \cr & f\left( 3 \right) = \int_1^3 {x\left( {{x^2} - 3x + 2} \right)dx} = \left[ {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right]_1^3 = 2 \cr & \therefore \max f\left( x \right) = 2.\,\,{\text{So, the range }} = \left[ { - \frac{1}{4},\,2} \right] \cr} $$
$$\eqalign{ & f'\left( x \right) = x\left( {{x^2} - 3x + 2} \right) = x\left( {x - 1} \right)\left( {x - 2} \right) \cr & {\text{The sign scheme for}}\,{\text{ }}f'\left( x \right){\text{ is as below}}{\text{.}} \cr} $$
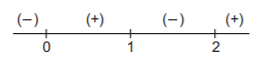
$$\eqalign{ & \therefore f'\left( x \right) \leqslant 0{\text{ in }}1 \leqslant x \leqslant 2{\text{ and }}f'\left( x \right) \geqslant 0{\text{ in }}2 \leqslant x \leqslant 3 \cr & \therefore f\left( x \right)\,{\text{is m}}{\text{.d}}{\text{. in }}\left[ {1,\,2} \right]{\text{ and m}}{\text{.i}}{\text{. in }}\left[ {2,\,3} \right] \cr & \therefore \min f\left( x \right) = f\left( 2 \right) = \int_1^2 {x\left( {{x^2} - 3x + 2} \right)dx} \cr & = \left[ {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right]_1^2 \cr & = - \frac{1}{4} \cr & \max f\left( x \right) = {\text{the greatest among}}\left\{ {f\left( 1 \right),\,f\left( 3 \right)} \right\} \cr & f\left( 1 \right) = \int_1^1 {x\left( {{x^2} - 3x + 2} \right)dx} = 0 \cr & f\left( 3 \right) = \int_1^3 {x\left( {{x^2} - 3x + 2} \right)dx} = \left[ {\frac{{{x^4}}}{4} - {x^3} + {x^2}} \right]_1^3 = 2 \cr & \therefore \max f\left( x \right) = 2.\,\,{\text{So, the range }} = \left[ { - \frac{1}{4},\,2} \right] \cr} $$