Question
Let $$f:R \to R$$ be a function defined by $$f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}.$$ The set of all points where $$f\left( x \right)$$ is NOT differentiable is-
A.
$$\left\{ { - 1,\,1} \right\}$$
B.
$$\left\{ { - 1,\,0} \right\}$$
C.
$$\left\{ {0,\,1} \right\}$$
D.
$$\left\{ { - 1,\,0,\,1} \right\}$$
Answer :
$$\left\{ { - 1,\,0,\,1} \right\}$$
Solution :
\[\begin{array}{l} f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}\\ = \left\{ \begin{array}{l} x\,\,\,\,;\,\,x < - 1\\ {x^3}\,\,;\,\, - 1 \le x \le 0\\ x\,\,\,\,;\,\,0 \le x \le 1\\ {x^3}\,\,;\,\,x \ge 1 \end{array} \right. \end{array}\]
KEY CONCEPT
A continuous function $$f\left( x \right)$$ is not differentiable at $$x= a$$
If graphically it takes a sharp turn at $$x=a.$$
Graph of $$f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}$$ is as shown with solid lines.
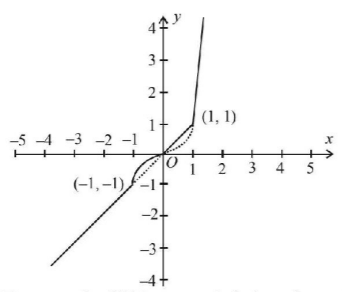
From graph of $$f\left( x \right)$$ at $$x =-1, \,0, \,1,$$ we have sharp turns.
$$\therefore f\left( x \right)$$ is not differentiable at $$x =- 1, \,0, \,1.$$
\[\begin{array}{l} f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}\\ = \left\{ \begin{array}{l} x\,\,\,\,;\,\,x < - 1\\ {x^3}\,\,;\,\, - 1 \le x \le 0\\ x\,\,\,\,;\,\,0 \le x \le 1\\ {x^3}\,\,;\,\,x \ge 1 \end{array} \right. \end{array}\]
KEY CONCEPT
A continuous function $$f\left( x \right)$$ is not differentiable at $$x= a$$
If graphically it takes a sharp turn at $$x=a.$$
Graph of $$f\left( x \right) = \max \,\left\{ {x,\,{x^3}} \right\}$$ is as shown with solid lines.

From graph of $$f\left( x \right)$$ at $$x =-1, \,0, \,1,$$ we have sharp turns.
$$\therefore f\left( x \right)$$ is not differentiable at $$x =- 1, \,0, \,1.$$