Question
Let $$d_1, d_2$$ and $$d_3$$ be the lengths of perpendiculars from circumcentre of $$\Delta \,ABC$$ on the sides $$BC, AC$$ and $$AB,$$ respectively. If $$ \lambda \left( {\frac{a}{{{d_1}}} + \frac{b}{{{d_2}}} + \frac{c}{{{d_3}}}} \right) = \frac{{abc}}{{{d_1}{d_2}{d_3}}}\,$$ then $$\lambda $$ equals
A.
1
B.
2
C.
3
D.
4
Answer :
4
Solution :
$$\eqalign{ & {\text{We have, }}\,\tan A = \frac{a}{{2{d_1}}}; \cr & {d_1} = R\cos A\,{\text{ etc}}{\text{.}} \cr} $$
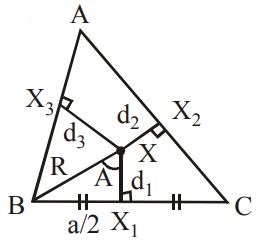
$$\eqalign{ & {\text{Similarly, }}\,\tan B = \frac{b}{{2{d_2}}} \cr & {\text{and }}\,\tan C = \frac{C}{{2{d_3}}} \cr & {\text{In }}\,\Delta \,ABC,\tan A + \tan B + \tan C \cr & = \tan A \cdot \tan B \cdot \tan C \cr & \Rightarrow \frac{a}{{2{d_1}}} + \frac{b}{{2{d_2}}} + \frac{c}{{2{d_3}}} = \frac{{abc}}{{8{d_1}{d_2}{d_3}}} \cr & \therefore 4\left( {\frac{a}{{{d_1}}} + \frac{b}{{{d_2}}} + \frac{c}{{{d_3}}}} \right) = \frac{{abc}}{{{d_1}{d_2}{d_3}}} \cr & \Rightarrow \lambda = 4 \cr} $$
$$\eqalign{ & {\text{We have, }}\,\tan A = \frac{a}{{2{d_1}}}; \cr & {d_1} = R\cos A\,{\text{ etc}}{\text{.}} \cr} $$

$$\eqalign{ & {\text{Similarly, }}\,\tan B = \frac{b}{{2{d_2}}} \cr & {\text{and }}\,\tan C = \frac{C}{{2{d_3}}} \cr & {\text{In }}\,\Delta \,ABC,\tan A + \tan B + \tan C \cr & = \tan A \cdot \tan B \cdot \tan C \cr & \Rightarrow \frac{a}{{2{d_1}}} + \frac{b}{{2{d_2}}} + \frac{c}{{2{d_3}}} = \frac{{abc}}{{8{d_1}{d_2}{d_3}}} \cr & \therefore 4\left( {\frac{a}{{{d_1}}} + \frac{b}{{{d_2}}} + \frac{c}{{{d_3}}}} \right) = \frac{{abc}}{{{d_1}{d_2}{d_3}}} \cr & \Rightarrow \lambda = 4 \cr} $$