Question
Let $$d$$ be the perpendicular distance from the centre of the ellipse $$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$$ to the tangent drawn at a point $$P$$ on the ellipse. If $${F_1}$$ and $${F_2}$$ be the foci of the ellipse, then $${\left( {P{F_1} - P{F_2}} \right)^2} = ?$$
A.
$$4{a^2}\left( {1 - \frac{{{b^2}}}{{{d^2}}}} \right)$$
B.
$${a^2}\left( {1 - \frac{{{b^2}}}{{{d^2}}}} \right)$$
C.
$$4{b^2}\left( {1 - \frac{{{a^2}}}{{{d^2}}}} \right)$$
D.
$${b^2}\left( {1 - \frac{{{a^2}}}{{{d^2}}}} \right)$$
Answer :
$$4{a^2}\left( {1 - \frac{{{b^2}}}{{{d^2}}}} \right)$$
Solution :
Let the point $$P$$ be $$\left( {a\,\cos \,\theta ,\,b\,\sin \,\theta } \right)$$
The equation of tangent at $$P$$ is
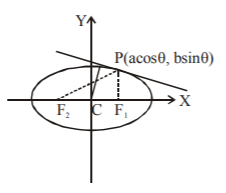
$$\frac{{x\,\cos \,\theta }}{a} + \frac{{y\,\sin \,\theta }}{b} = 1......\left( 1 \right)$$
If $$d$$ be the length of perpendicular from the centre $$C\left( {0,\,0} \right)$$ of the ellipse to the tangent given by $$\left( 1 \right)$$ then
$$\eqalign{ & d = \frac{1}{{\sqrt {\frac{{{{\cos }^2}\theta }}{{{a^2}}} + \frac{{{{\sin }^2}\theta }}{{{b^2}}}} }} \cr & \Rightarrow \frac{1}{{{d^2}}} = \frac{{{{\cos }^2}\theta }}{{{a^2}}} + \frac{{{{\sin }^2}\theta }}{{{b^2}}} \cr & \Rightarrow \frac{{{b^2}}}{{{d^2}}} = \frac{{{b^2}}}{{{a^2}}}{\cos ^2}\theta + 1 - {\cos ^2}\theta \cr & \Rightarrow 1 - \frac{{{b^2}}}{{{d^2}}} = \left( {1 - \frac{{{b^2}}}{{{a^2}}}} \right){\cos ^2}\theta \cr & \Rightarrow 1 - \frac{{{b^2}}}{{{d^2}}} = {e^2}{\cos ^2}\theta ......\left( 2 \right) \cr & {\text{Now,}}\,\,{\left( {P{F_1} - P{F_2}} \right)^2} \cr & = {\left( {2ae\,\cos \,\theta } \right)^2} \cr & = 4{a^2}{e^2}{\cos ^2}\theta \cr & = 4{a^2}\left( {1 - \frac{{{b^2}}}{{{d^2}}}} \right) \cr} $$
Let the point $$P$$ be $$\left( {a\,\cos \,\theta ,\,b\,\sin \,\theta } \right)$$
The equation of tangent at $$P$$ is

$$\frac{{x\,\cos \,\theta }}{a} + \frac{{y\,\sin \,\theta }}{b} = 1......\left( 1 \right)$$
If $$d$$ be the length of perpendicular from the centre $$C\left( {0,\,0} \right)$$ of the ellipse to the tangent given by $$\left( 1 \right)$$ then
$$\eqalign{ & d = \frac{1}{{\sqrt {\frac{{{{\cos }^2}\theta }}{{{a^2}}} + \frac{{{{\sin }^2}\theta }}{{{b^2}}}} }} \cr & \Rightarrow \frac{1}{{{d^2}}} = \frac{{{{\cos }^2}\theta }}{{{a^2}}} + \frac{{{{\sin }^2}\theta }}{{{b^2}}} \cr & \Rightarrow \frac{{{b^2}}}{{{d^2}}} = \frac{{{b^2}}}{{{a^2}}}{\cos ^2}\theta + 1 - {\cos ^2}\theta \cr & \Rightarrow 1 - \frac{{{b^2}}}{{{d^2}}} = \left( {1 - \frac{{{b^2}}}{{{a^2}}}} \right){\cos ^2}\theta \cr & \Rightarrow 1 - \frac{{{b^2}}}{{{d^2}}} = {e^2}{\cos ^2}\theta ......\left( 2 \right) \cr & {\text{Now,}}\,\,{\left( {P{F_1} - P{F_2}} \right)^2} \cr & = {\left( {2ae\,\cos \,\theta } \right)^2} \cr & = 4{a^2}{e^2}{\cos ^2}\theta \cr & = 4{a^2}\left( {1 - \frac{{{b^2}}}{{{d^2}}}} \right) \cr} $$