Question
Let a vertical tower $$AB$$ have its end $$A$$ on the level ground. Let $$C$$ be the mid - point of $$AB$$ and $$P$$ be a point on the ground such that $$AP = 2AB.$$ If $$\angle BPC = \beta ,$$ then $$\tan\beta $$ is equal to:
A.
$$\frac{4}{9}$$
B.
$$\frac{6}{7}$$
C.
$$\frac{1}{4}$$
D.
$$\frac{2}{9}$$
Answer :
$$\frac{2}{9}$$
Solution :
$$\eqalign{ & {\text{Since }}AP = 2AB \cr & \Rightarrow \,\,\frac{{AB}}{{AP}} = \frac{1}{2}\,\,\,\,\,\,.....\left( 1 \right) \cr & {\text{Let }}\angle APC = \alpha \cr & \tan \alpha = \frac{{AC}}{{AP}} \cr & = \frac{1}{2}\frac{{AB}}{{AP}} \cr & = \frac{1}{4} \cr & \left( {\because \,C\,\,{\text{is the mid point }}\therefore \,AC = \frac{1}{2}AB} \right) \cr & \Rightarrow \,\,\tan \alpha = \frac{1}{4} \cr} $$
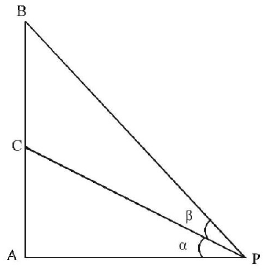
$$\eqalign{ & {\text{As }}\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \cr & \Rightarrow \,\,\frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \cr} $$
\[ = \frac{1}{2}\left[ \begin{gathered} \because \,\tan \left( {\alpha + \beta } \right) = \frac{{AB}}{{AP}} \hfill \\ \tan \left( {\alpha + \beta } \right) = \frac{1}{2}\left[ {{\text{From}}\left( 1 \right)} \right] \hfill \\ \end{gathered} \right]\]
$$\eqalign{ & \Rightarrow \,\,\frac{{\frac{1}{4} + \tan \beta }}{{1 - \frac{1}{4}\tan \beta }} = \frac{1}{2} \cr & \therefore \,\,\tan \beta = \frac{2}{9} \cr} $$
$$\eqalign{ & {\text{Since }}AP = 2AB \cr & \Rightarrow \,\,\frac{{AB}}{{AP}} = \frac{1}{2}\,\,\,\,\,\,.....\left( 1 \right) \cr & {\text{Let }}\angle APC = \alpha \cr & \tan \alpha = \frac{{AC}}{{AP}} \cr & = \frac{1}{2}\frac{{AB}}{{AP}} \cr & = \frac{1}{4} \cr & \left( {\because \,C\,\,{\text{is the mid point }}\therefore \,AC = \frac{1}{2}AB} \right) \cr & \Rightarrow \,\,\tan \alpha = \frac{1}{4} \cr} $$

$$\eqalign{ & {\text{As }}\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \cr & \Rightarrow \,\,\frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \cr} $$
\[ = \frac{1}{2}\left[ \begin{gathered} \because \,\tan \left( {\alpha + \beta } \right) = \frac{{AB}}{{AP}} \hfill \\ \tan \left( {\alpha + \beta } \right) = \frac{1}{2}\left[ {{\text{From}}\left( 1 \right)} \right] \hfill \\ \end{gathered} \right]\]
$$\eqalign{ & \Rightarrow \,\,\frac{{\frac{1}{4} + \tan \beta }}{{1 - \frac{1}{4}\tan \beta }} = \frac{1}{2} \cr & \therefore \,\,\tan \beta = \frac{2}{9} \cr} $$