Question
Let $$0 < \alpha < \frac{\pi }{2}$$ be a fixed angle. If $$P\left( {\cos \,\theta ,\,\sin \,\theta } \right)$$ and $$Q\left( {\cos \left( {\alpha - \theta } \right),\,\sin \left( {\alpha - \theta } \right)} \right),$$ then $$Q$$ is obtained from $$P$$ by the :
A.
clockwise rotation around the origin through an angle $$\alpha $$
B.
anticlockwise rotation around the origin through an angle $$\alpha $$
C.
reflection in the line through the origin with slope $$\tan \,\alpha $$
D.
reflection in the line through the origin with slope $$\tan \left( {\frac{\alpha }{2}} \right)$$
Answer :
reflection in the line through the origin with slope $$\tan \left( {\frac{\alpha }{2}} \right)$$
Solution :
Clearly, $$OP = OQ = 1$$ and $$\angle QOP = \alpha - \theta - \theta = \alpha - 2\theta $$
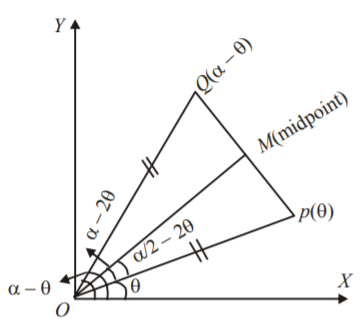
The bisector of $$\angle QOP$$ will be perpendicular to $$PQ$$ and also bisect it. Hence, $$Q$$ is the reflection of $$P$$ in the line $$OM$$ which makes an angle equal to $$\angle MOP + \angle POX$$ with the $$x$$-axis, i.e., $$\frac{1}{2}\left( {\alpha - 2\theta } \right) + \theta = \frac{\alpha }{2}$$
So that slope of $$OM$$ is $$\tan \left( {\frac{\alpha }{2}} \right).$$
Clearly, $$OP = OQ = 1$$ and $$\angle QOP = \alpha - \theta - \theta = \alpha - 2\theta $$

The bisector of $$\angle QOP$$ will be perpendicular to $$PQ$$ and also bisect it. Hence, $$Q$$ is the reflection of $$P$$ in the line $$OM$$ which makes an angle equal to $$\angle MOP + \angle POX$$ with the $$x$$-axis, i.e., $$\frac{1}{2}\left( {\alpha - 2\theta } \right) + \theta = \frac{\alpha }{2}$$
So that slope of $$OM$$ is $$\tan \left( {\frac{\alpha }{2}} \right).$$