Question
Kirchhoff’s first law, i.e. $$\sum i = 0$$ at a junction, deals with the conservation of
A.
angular momentum
B.
linear momentum
C.
energy
D.
charge
Answer :
charge
Solution :
Kirchhoff’s law states that the algebraic sum of currents meeting at a point (say at a junction) is equals to zero i.e.,
$$\sum i = 0$$
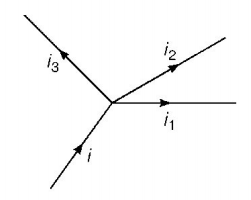
or $$i = {i_1} + {i_2} + {i_3}$$
$$\eqalign{ & \frac{{dQ}}{{dt}} = \frac{{d{Q_1}}}{{dt}} + \frac{{d{Q_2}}}{{dt}} + \frac{{d{Q_3}}}{{dt}} \cr & {\text{or}}\,\,dQ = d{Q_1} + d{Q_2} + d{Q_3} \cr} $$
So, we can say that when a steady current flows through circuit, then neither accumulation of charges takes place at the junction in the circuit nor any charge is removed from there. That’s why Kirchhoff's first law deals with the conservation of charge.
Kirchhoff’s law states that the algebraic sum of currents meeting at a point (say at a junction) is equals to zero i.e.,
$$\sum i = 0$$

or $$i = {i_1} + {i_2} + {i_3}$$
$$\eqalign{ & \frac{{dQ}}{{dt}} = \frac{{d{Q_1}}}{{dt}} + \frac{{d{Q_2}}}{{dt}} + \frac{{d{Q_3}}}{{dt}} \cr & {\text{or}}\,\,dQ = d{Q_1} + d{Q_2} + d{Q_3} \cr} $$
So, we can say that when a steady current flows through circuit, then neither accumulation of charges takes place at the junction in the circuit nor any charge is removed from there. That’s why Kirchhoff's first law deals with the conservation of charge.
