Question
In young's double - slit experiment, the separation between the slits is $$d,$$ distance between the slit and screen is $$D\left( {D > > D} \right).$$ In the interference pattern, there is a maxima exactly in front of each slit. Then the possible wavelength(s) used. in the experiment are
A.
$$\frac{{{d^2}}}{D},\frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{3D}}$$
B.
$$\frac{{{d^2}}}{D},\frac{{{d^2}}}{{3D}},\frac{{{d^2}}}{{5D}}$$
C.
$$\frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{4D}},\frac{{{d^2}}}{{6D}}$$
D.
None of these
Answer :
$$\frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{4D}},\frac{{{d^2}}}{{6D}}$$
Solution :
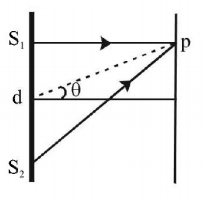
$$\eqalign{ & {S_2}P - {S_1}P = \frac{{dy}}{D} = \frac{{d \times \left( {\frac{d}{2}} \right)}}{D} = \frac{{{d^2}}}{{2D}} \cr & \frac{{{d^2}}}{{2D}} = n\lambda \cr & \lambda = \frac{{{d^2}}}{{2nD}},n = 1,2,....... \cr & \lambda = \frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{4D}},\frac{{{d^2}}}{{6D}} \cr} $$

$$\eqalign{ & {S_2}P - {S_1}P = \frac{{dy}}{D} = \frac{{d \times \left( {\frac{d}{2}} \right)}}{D} = \frac{{{d^2}}}{{2D}} \cr & \frac{{{d^2}}}{{2D}} = n\lambda \cr & \lambda = \frac{{{d^2}}}{{2nD}},n = 1,2,....... \cr & \lambda = \frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{4D}},\frac{{{d^2}}}{{6D}} \cr} $$