Question
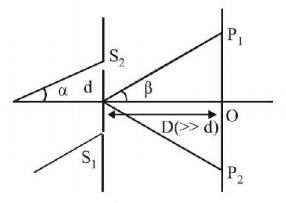
In $$YDSE$$ distance between the $${S_1}$$ and $${S_2}$$ is $$d.$$ $${P_1}$$ and $${P_2}$$ are two points equidistance from $$O$$ at an angular position $$\beta $$ as shown. A parallel beam of monochromatic light is incident at an angle $$\alpha $$ on the slits. Then the ratio of path difference at $${P_1}$$ and $${P_2}$$ is:
In $$YDSE$$ distance between the $${S_1}$$ and $${S_2}$$ is $$d.$$ $${P_1}$$ and $${P_2}$$ are two points equidistance from $$O$$ at an angular position $$\beta $$ as shown. A parallel beam of monochromatic light is incident at an angle $$\alpha $$ on the slits. Then the ratio of path difference at $${P_1}$$ and $${P_2}$$ is:
A.
$$\cot \frac{{\alpha - \beta }}{2}\cot \frac{{\alpha + \beta }}{2}$$
B.
$$\tan \frac{{\alpha + \beta }}{2}\cot \frac{{\alpha - \beta }}{2}$$
C.
$$\sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}$$
D.
$$\tan \frac{{\alpha - \beta }}{2}\cot \frac{{\alpha + \beta }}{2}$$
Answer :
$$\tan \frac{{\alpha - \beta }}{2}\cot \frac{{\alpha + \beta }}{2}$$
Solution :
$$\frac{{\Delta {P_1}}}{{\Delta {P_2}}} = \frac{{\sin \alpha - \sin \beta }}{{\sin \alpha + \sin \beta }} = \tan \frac{{\alpha - \beta }}{2}\cot \frac{{\alpha + \beta }}{2}$$
$$\frac{{\Delta {P_1}}}{{\Delta {P_2}}} = \frac{{\sin \alpha - \sin \beta }}{{\sin \alpha + \sin \beta }} = \tan \frac{{\alpha - \beta }}{2}\cot \frac{{\alpha + \beta }}{2}$$