Question
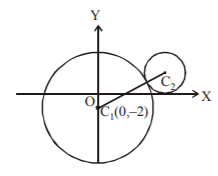
In the given figure, the equation of the larger circle is $${x^2} + {y^2} + 4y - 5 = 0$$ and the distance between centers is $$4.$$ Then the equation of smaller circle is
In the given figure, the equation of the larger circle is $${x^2} + {y^2} + 4y - 5 = 0$$ and the distance between centers is $$4.$$ Then the equation of smaller circle is
A.
$${\left( {x - \sqrt 7 } \right)^2} + {\left( {y - 1} \right)^2} = 1$$
B.
$${\left( {x + \sqrt 7 } \right)^2} + {\left( {y - 1} \right)^2} = 1$$
C.
$${x^2} + {y^2} = 2\sqrt 7 x + 2y$$
D.
None of these
Answer :
$${\left( {x - \sqrt 7 } \right)^2} + {\left( {y - 1} \right)^2} = 1$$
Solution :
We have $${x^2} + {y^2} + 4y - 5 = 0.$$
Its centre is $${C_1}\left( {0,\, - 2} \right),\,{r_1} = \sqrt {4 + 5} = 3$$
Let $${C_2}\left( {h,\,k} \right)$$ be the centre of the smaller circle and its radius $${r_2}.$$ Then, $${C_1}{C_2} = 4.$$
$$\eqalign{ & \Rightarrow \sqrt {{h^2} + {{\left( {k + 2} \right)}^2}} = 3 + {r_2} = 4......\left( 1 \right) \cr & \Rightarrow {r_2} = 1 \cr} $$
But $$k = {r_2} = 1$$ [it touches $$x$$-axis]
$$\therefore $$ From equation $$\left( 1 \right),$$ we get
$$\eqalign{ & 4 = \,\,\sqrt {{h^2} + {{\left( {1 + 2} \right)}^2}} \cr & \Rightarrow 16 = {h^2} + 9 \cr & \Rightarrow {h^2} = 7 \cr & \Rightarrow h = \pm \sqrt 7 \cr} $$
Since $$h > 0\,\,\,\,\,\therefore h = \sqrt 7 $$
Hence, required circle is $${\left( {x - \sqrt 7 } \right)^2} + {\left( {y - 1} \right)^2} = 1$$
We have $${x^2} + {y^2} + 4y - 5 = 0.$$
Its centre is $${C_1}\left( {0,\, - 2} \right),\,{r_1} = \sqrt {4 + 5} = 3$$
Let $${C_2}\left( {h,\,k} \right)$$ be the centre of the smaller circle and its radius $${r_2}.$$ Then, $${C_1}{C_2} = 4.$$
$$\eqalign{ & \Rightarrow \sqrt {{h^2} + {{\left( {k + 2} \right)}^2}} = 3 + {r_2} = 4......\left( 1 \right) \cr & \Rightarrow {r_2} = 1 \cr} $$
But $$k = {r_2} = 1$$ [it touches $$x$$-axis]
$$\therefore $$ From equation $$\left( 1 \right),$$ we get
$$\eqalign{ & 4 = \,\,\sqrt {{h^2} + {{\left( {1 + 2} \right)}^2}} \cr & \Rightarrow 16 = {h^2} + 9 \cr & \Rightarrow {h^2} = 7 \cr & \Rightarrow h = \pm \sqrt 7 \cr} $$
Since $$h > 0\,\,\,\,\,\therefore h = \sqrt 7 $$
Hence, required circle is $${\left( {x - \sqrt 7 } \right)^2} + {\left( {y - 1} \right)^2} = 1$$