Question
In the figure ammeter $${A_1}$$ reads a current of $$10\,mA,$$ while the voltmeter reads a potential difference of $$3V.$$ What does ammeter $${A_2}$$ in $$mA$$ read ? The ammeters are identical, the internal resistance of the battery is negligible.
In the figure ammeter $${A_1}$$ reads a current of $$10\,mA,$$ while the voltmeter reads a potential difference of $$3V.$$ What does ammeter $${A_2}$$ in $$mA$$ read ? The ammeters are identical, the internal resistance of the battery is negligible.
(Consider all ammeters and voltmeters as non-ideal.)

A.
$$6.67\,mA$$
B.
$$3.12\,mA$$
C.
$$1.12\,mA$$
D.
$$5.14\,mA$$
Answer :
$$6.67\,mA$$
Solution :
$${R_A} = $$ resistance of ammeter
$$\eqalign{ & \frac{{4 - {V_1}}}{{100}} = \frac{{{V_1} - 1}}{{{R_A}}} + \frac{{{V_1} - 0}}{{100}}\,......\left( {\text{i}} \right) \cr & 1\,V - 0\,V = \left( {10mA} \right){R_A} \cr & {R_A} = 100\Omega \,......\left( {{\text{ii}}} \right) \cr} $$
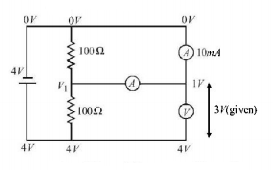
$$\eqalign{ & \frac{{4 - {V_1}}}{{100}} = \frac{{{V_1} - 1}}{{100}} + \frac{{{V_1} - 0}}{{100}}\,\,\left[ {{\text{By using eq}}{\text{. }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right)} \right] \cr & {V_1} = \left( {\frac{5}{3}} \right)V \cr & \frac{{{V_1} - 1}}{{{R_A}}} = \left( {{\text{Current in ammeter }}\left( {{\text{II}}} \right)} \right) \cr & = \frac{{\left( {\frac{5}{3}} \right) - 1}}{{100}} = 6.67\,mA \cr} $$
$${R_A} = $$ resistance of ammeter
$$\eqalign{ & \frac{{4 - {V_1}}}{{100}} = \frac{{{V_1} - 1}}{{{R_A}}} + \frac{{{V_1} - 0}}{{100}}\,......\left( {\text{i}} \right) \cr & 1\,V - 0\,V = \left( {10mA} \right){R_A} \cr & {R_A} = 100\Omega \,......\left( {{\text{ii}}} \right) \cr} $$

$$\eqalign{ & \frac{{4 - {V_1}}}{{100}} = \frac{{{V_1} - 1}}{{100}} + \frac{{{V_1} - 0}}{{100}}\,\,\left[ {{\text{By using eq}}{\text{. }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right)} \right] \cr & {V_1} = \left( {\frac{5}{3}} \right)V \cr & \frac{{{V_1} - 1}}{{{R_A}}} = \left( {{\text{Current in ammeter }}\left( {{\text{II}}} \right)} \right) \cr & = \frac{{\left( {\frac{5}{3}} \right) - 1}}{{100}} = 6.67\,mA \cr} $$
