Question
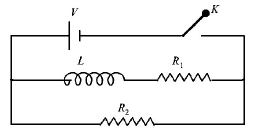
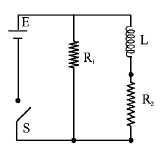
In the circuit shown below, the key $$K$$ is closed at $$t = 0.$$ The current through the battery is
In the circuit shown below, the key $$K$$ is closed at $$t = 0.$$ The current through the battery is
A.
$$\frac{{V{R_1}{R_2}}}{{\sqrt {R_1^2 + R_2^2} }}\,{\text{at}}\,t = 0\,{\text{and}}\,\frac{V}{{{R_2}}}\,{\text{at}}\,t = \infty $$
B.
$$\frac{V}{{{R_2}}}\,{\text{at}}\,t = 0\,{\text{and}}\,\frac{{V\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2}}}\,{\text{at}}\,t = \infty $$
C.
$$\frac{V}{{{R_2}}}\,{\text{at}}\,t = 0\,{\text{and}}\,\frac{{V{R_1}{R_2}}}{{\sqrt {R_1^2 + R_2^2} }}\,{\text{at}}\,t = \infty $$
D.
$$\frac{{V\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2}}}\,{\text{at}}\,t = 0\,{\text{and}}\,\frac{V}{{{R_2}}}\,{\text{at}}\,t = \infty $$
Answer :
$$\frac{V}{{{R_2}}}\,{\text{at}}\,t = 0\,{\text{and}}\,\frac{{V{R_1}{R_2}}}{{\sqrt {R_1^2 + R_2^2} }}\,{\text{at}}\,t = \infty $$
Solution :
At $$t$$ = 0, no current will flow through $$L$$ and $${R_1}$$
∴ Current through battery = $$\frac{V}{{{R_2}}}$$
At $$\,t = \infty ,$$
effective resistance, $${R_{eff}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$$
∴ Current through battery = $$\frac{V}{{{R_{eff}}}} = \frac{{V\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2}}}$$
At $$t$$ = 0, no current will flow through $$L$$ and $${R_1}$$
∴ Current through battery = $$\frac{V}{{{R_2}}}$$
At $$\,t = \infty ,$$
effective resistance, $${R_{eff}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$$
∴ Current through battery = $$\frac{V}{{{R_{eff}}}} = \frac{{V\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2}}}$$
