Question
In the circuit of figure, the current in $$4\,\Omega $$ resistance is $$1.2\,A,$$ what is the potential difference between $$B$$ and $$C$$ ?
In the circuit of figure, the current in $$4\,\Omega $$ resistance is $$1.2\,A,$$ what is the potential difference between $$B$$ and $$C$$ ?

A.
$$3.6\,V$$
B.
$$6.3\,V$$
C.
$$1.8\,V$$
D.
$$2.4\,V$$
Answer :
$$3.6\,V$$
Solution :
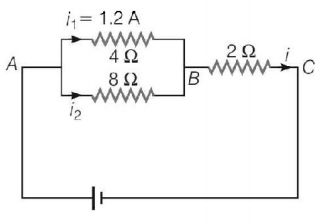
The potential difference across $$4\,\Omega $$ resistance given by Ohm's law
$$\eqalign{ & = 4 \times {i_1} \cr & = 4 \times 1.2 = 4.8\,V\,\,\left( {{\text{as}}\,{i_1} = 1.2\,A} \right) \cr} $$
As resistances $$4\,\Omega $$ and $$8\,\Omega $$ are in parallel, so potential difference across $$8\,\Omega $$ resistance will also be $$4.8\,V.$$
$$\therefore $$ Current through $$8\,\Omega $$ resistance
$$\eqalign{ & {i_2} = \frac{V}{R} = \frac{{4.8}}{8} = 0.6\,A \cr & \therefore i = {i_1} + {i_2} = 1.2 + 0.6 = 1.8\,A \cr} $$
$$\therefore $$ Potential difference across $$2\,\Omega $$ resistance
$$\eqalign{ & {V_{BC}} = i \times 2 \cr & = 1.8 \times 2 = 3.6\,V \cr} $$

The potential difference across $$4\,\Omega $$ resistance given by Ohm's law
$$\eqalign{ & = 4 \times {i_1} \cr & = 4 \times 1.2 = 4.8\,V\,\,\left( {{\text{as}}\,{i_1} = 1.2\,A} \right) \cr} $$
As resistances $$4\,\Omega $$ and $$8\,\Omega $$ are in parallel, so potential difference across $$8\,\Omega $$ resistance will also be $$4.8\,V.$$
$$\therefore $$ Current through $$8\,\Omega $$ resistance
$$\eqalign{ & {i_2} = \frac{V}{R} = \frac{{4.8}}{8} = 0.6\,A \cr & \therefore i = {i_1} + {i_2} = 1.2 + 0.6 = 1.8\,A \cr} $$
$$\therefore $$ Potential difference across $$2\,\Omega $$ resistance
$$\eqalign{ & {V_{BC}} = i \times 2 \cr & = 1.8 \times 2 = 3.6\,V \cr} $$
