Question
In the adjacent diagram, $$CP$$ represents a wave front and $$AO$$ & $$BP,$$ the corresponding two rays. Find the condition on $$\theta $$ for constructive interference at $$P$$ between the ray $$BP$$ and reflected ray $$OP.$$
In the adjacent diagram, $$CP$$ represents a wave front and $$AO$$ & $$BP,$$ the corresponding two rays. Find the condition on $$\theta $$ for constructive interference at $$P$$ between the ray $$BP$$ and reflected ray $$OP.$$

A.
$$\cos \theta = \frac{{3\,\lambda }}{{2\,d}}$$
B.
$$\cos \theta = \frac{{\lambda }}{{4\,d}}$$
C.
$$sec\theta - \cos \theta = \frac{\lambda }{d}$$
D.
$$sec\theta - \cos \theta = \frac{4\,\lambda }{d}$$
Answer :
$$\cos \theta = \frac{{\lambda }}{{4\,d}}$$
Solution :
$$\eqalign{ & {\text{In }}\Delta \,OPM,\,\,OP = \frac{d}{{\cos \theta }} \cr & {\text{In }}\Delta \,COP,\,OC = \frac{{d\cos 2\,\theta }}{{\cos \theta }} \cr} $$
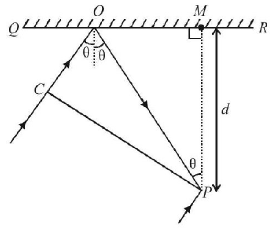
Path difference between the two rays reaching $$P$$ is
$$\eqalign{ & = CO + OP + \frac{\lambda }{2} = \frac{{d\cos 2\,\theta }}{{\cos \theta }} + \frac{d}{{\cos \theta }} + \frac{\lambda }{2} \cr & = \frac{d}{{\cos \theta }}\left( {\cos 2\,\theta + 1} \right) + \frac{\lambda }{2} = 2\,d\cos \theta + \frac{\lambda }{2} \cr} $$
For constructive interference, path difference should be $$n\lambda $$
$$\eqalign{ & \therefore \,\,2\,d\cos \theta + \frac{\lambda }{2} = n\lambda \cr & \Rightarrow \,\,\cos \theta = \frac{{\left( {2\,n - 1} \right)}}{4}\frac{\lambda }{d} \cr & {\text{For, }}n = 1,\cos \theta = \frac{\lambda }{{4\,d}} \cr} $$
$$\eqalign{ & {\text{In }}\Delta \,OPM,\,\,OP = \frac{d}{{\cos \theta }} \cr & {\text{In }}\Delta \,COP,\,OC = \frac{{d\cos 2\,\theta }}{{\cos \theta }} \cr} $$

Path difference between the two rays reaching $$P$$ is
$$\eqalign{ & = CO + OP + \frac{\lambda }{2} = \frac{{d\cos 2\,\theta }}{{\cos \theta }} + \frac{d}{{\cos \theta }} + \frac{\lambda }{2} \cr & = \frac{d}{{\cos \theta }}\left( {\cos 2\,\theta + 1} \right) + \frac{\lambda }{2} = 2\,d\cos \theta + \frac{\lambda }{2} \cr} $$
For constructive interference, path difference should be $$n\lambda $$
$$\eqalign{ & \therefore \,\,2\,d\cos \theta + \frac{\lambda }{2} = n\lambda \cr & \Rightarrow \,\,\cos \theta = \frac{{\left( {2\,n - 1} \right)}}{4}\frac{\lambda }{d} \cr & {\text{For, }}n = 1,\cos \theta = \frac{\lambda }{{4\,d}} \cr} $$