Question
In $$\Delta ABC$$ the mid-point of the sides $$AB,\,BC$$ and $$CA$$ are respectively $$\left( {l,\,0,\,0} \right),\,\left( {0,\,m,\,0} \right)$$ and $$\left( {0,\,0,\,n} \right).$$
In $$\Delta ABC$$ the mid-point of the sides $$AB,\,BC$$ and $$CA$$ are respectively $$\left( {l,\,0,\,0} \right),\,\left( {0,\,m,\,0} \right)$$ and $$\left( {0,\,0,\,n} \right).$$
Then, $$\frac{{A{B^2} + B{C^2} + C{A^2}}}{{{l^2} + {m^2} + {n^2}}}$$ is equal to :
A.
2
B.
4
C.
8
D.
16
Answer :
8
Solution :
$${\text{From the figure}}$$
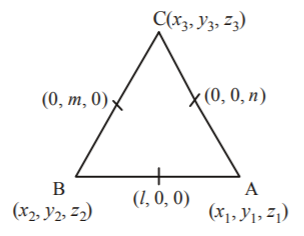
$$\eqalign{ & {x_1} + {x_2} = 2l,\,{y_1} + {y_2} = 0,\,{z_1} + {z_2} = 0 \cr & {x_2} + {x_3} = 0,\,{y_2} + {y_3} = 2m,\,{z_1} + {z_3} = 0 \cr & {\text{and }}{x_1} + {x_3} = 0,\,{y_1} + {y_3} = 0,\,{z_1} + {z_3} = 2n \cr & {\text{On solving, we get}} \cr & {x_1} = l,\,{x_2} = l,\,{x_3} = - l \cr & {y_1} = - m,\,{y_2} = m,\,{y_3} = m \cr & {\text{and }}{z_1} = n,\,{z_2} = - n,\,{z_3} = n \cr & \therefore \,{\text{Coordinates are}}\,: \cr & A\left( {l,\, - m,\,n} \right),\,B\left( {l,\,m,\, - n} \right){\text{and }}C\left( { - l,\,m,\,n} \right) \cr & \therefore \,\frac{{A{B^2} + B{C^2} + C{A^2}}}{{{l^2} + {m^2} + {n^2}}} \cr & = \frac{{\left( {4{m^2} + 4{n^2}} \right) + \left( {4{l^2} + 4{n^2}} \right) + \left( {4{l^2} + 4{m^2}} \right)}}{{{l^2} + {m^2} + {n^2}}} \cr & = 8 \cr} $$
$${\text{From the figure}}$$
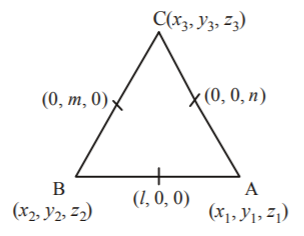
$$\eqalign{ & {x_1} + {x_2} = 2l,\,{y_1} + {y_2} = 0,\,{z_1} + {z_2} = 0 \cr & {x_2} + {x_3} = 0,\,{y_2} + {y_3} = 2m,\,{z_1} + {z_3} = 0 \cr & {\text{and }}{x_1} + {x_3} = 0,\,{y_1} + {y_3} = 0,\,{z_1} + {z_3} = 2n \cr & {\text{On solving, we get}} \cr & {x_1} = l,\,{x_2} = l,\,{x_3} = - l \cr & {y_1} = - m,\,{y_2} = m,\,{y_3} = m \cr & {\text{and }}{z_1} = n,\,{z_2} = - n,\,{z_3} = n \cr & \therefore \,{\text{Coordinates are}}\,: \cr & A\left( {l,\, - m,\,n} \right),\,B\left( {l,\,m,\, - n} \right){\text{and }}C\left( { - l,\,m,\,n} \right) \cr & \therefore \,\frac{{A{B^2} + B{C^2} + C{A^2}}}{{{l^2} + {m^2} + {n^2}}} \cr & = \frac{{\left( {4{m^2} + 4{n^2}} \right) + \left( {4{l^2} + 4{n^2}} \right) + \left( {4{l^2} + 4{m^2}} \right)}}{{{l^2} + {m^2} + {n^2}}} \cr & = 8 \cr} $$