Question
In an optics experiment, with the position of the object fixed, a student varies the position of a convex lens and for each position, the screen is adjusted to get a clear image of the object. A graph between the object distance $$u$$ and the image distance $$v,$$ from the lens, is plotted using the same scale for the two axes. A straight line passing through the origin and making an angle of 45° with the $$x$$ - axis meets the experimental curve at $$P.$$ The coordinates of $$P$$ will be:
A.
$$\left( {\frac{f}{2},\frac{f}{2}} \right)$$
B.
$$\left( {f,f} \right)$$
C.
$$\left( {4\,f, 4\,f} \right)$$
D.
$$\left( {2\,f, 2\,f} \right)$$
Answer :
$$\left( {2\,f, 2\,f} \right)$$
Solution :
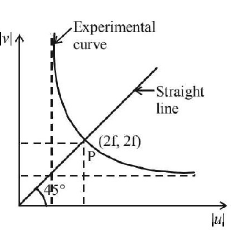
Here $$u = - 2\,f, v = 2\,f$$
As $$\left| u \right|$$ increases, $$v$$ decreases for $$\left| u \right|$$ $$> f.$$ The graph between $$\left| v \right|$$ and $$\left| u \right|$$ is shown in the figure. A straight line passing through the origin and making an angle of 45° with the $$x$$ - axis meets the experimental curve at $$P(2\,f, 2\,f).$$

Here $$u = - 2\,f, v = 2\,f$$
As $$\left| u \right|$$ increases, $$v$$ decreases for $$\left| u \right|$$ $$> f.$$ The graph between $$\left| v \right|$$ and $$\left| u \right|$$ is shown in the figure. A straight line passing through the origin and making an angle of 45° with the $$x$$ - axis meets the experimental curve at $$P(2\,f, 2\,f).$$

