Question
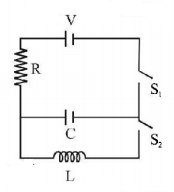
In an $$LCR$$ circuit as shown below both switches are open initially. Now switch $${S_1}$$ is closed, $${S_2}$$ kept open. ($$q$$ is charge on the capacitor and $$\tau = RC$$ is Capacitive time constant). Which of the following statements is correct ?
In an $$LCR$$ circuit as shown below both switches are open initially. Now switch $${S_1}$$ is closed, $${S_2}$$ kept open. ($$q$$ is charge on the capacitor and $$\tau = RC$$ is Capacitive time constant). Which of the following statements is correct ?
A.
At, $$t = 0,q = CV\left( {1 - e} \right)$$
B.
At, $$t = \tau ,q = \frac{{CV}}{2}$$
C.
At, $$t = 2\tau ,q = CV\left( {1 - {e^{ - 2}}} \right)$$
D.
At, $$t = 2\tau ,q = CV\left( {1 - {e^{ - 1}}} \right)$$
Answer :
At, $$t = 2\tau ,q = CV\left( {1 - {e^{ - 2}}} \right)$$
Solution :
Charge on he capacitor at any time $$t$$ is given by $$q = CV\left( {1 - {e^{\frac{t}{\tau }}}} \right)\,\,{\text{at}}\,\,t = 2\tau $$
$$q = CV\left( {1 - {e^{ - 2}}} \right)$$
Charge on he capacitor at any time $$t$$ is given by $$q = CV\left( {1 - {e^{\frac{t}{\tau }}}} \right)\,\,{\text{at}}\,\,t = 2\tau $$
$$q = CV\left( {1 - {e^{ - 2}}} \right)$$