Question
In an equilateral triangle, 3 coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. Area of the triangle is
In an equilateral triangle, 3 coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. Area of the triangle is

A.
$$4 + 2\sqrt 3 $$
B.
$$6 + 4\sqrt 3 $$
C.
$$12 + \frac{{7\sqrt 3 }}{4}$$
D.
$$3 + \frac{{7\sqrt 3 }}{4}$$
Answer :
$$6 + 4\sqrt 3 $$
Solution :
The situation is as shown in the figure. For circle with centre $${C_2},BP$$ and $$BP'$$ are two tangents from $$B$$ to circle, therefore $$B{C_2}$$ must be the $$\angle$$ bisector of $$\angle B.$$ But $$\angle B = 60°$$ $$\left( {\because \,\,\Delta ABC\,\,{\text{is an equilateral}}\,\,\Delta } \right)$$
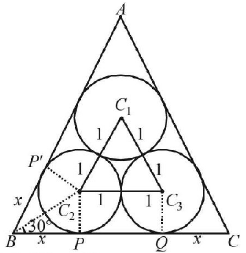
$$\eqalign{ & \therefore \,\,\angle {C_2}BP = {30^ \circ } \cr & \therefore \,\,\tan {30^ \circ } = \frac{1}{x} \cr & \Rightarrow \,\,x = \sqrt 3 \cr & \therefore \,\,BC = BP + PQ + QC \cr & = x + 2 + x = 2 + 2\sqrt 3 \cr & \therefore \,\,{\text{Area of }}\Delta ABC = \frac{{\sqrt 3 }}{4} \times {\left( {2 + 2\sqrt 3 } \right)^2} \cr & = 4\sqrt 3 + 6\,\,{\text{sq}}{\text{. units}}{\text{.}} \cr} $$
The situation is as shown in the figure. For circle with centre $${C_2},BP$$ and $$BP'$$ are two tangents from $$B$$ to circle, therefore $$B{C_2}$$ must be the $$\angle$$ bisector of $$\angle B.$$ But $$\angle B = 60°$$ $$\left( {\because \,\,\Delta ABC\,\,{\text{is an equilateral}}\,\,\Delta } \right)$$

$$\eqalign{ & \therefore \,\,\angle {C_2}BP = {30^ \circ } \cr & \therefore \,\,\tan {30^ \circ } = \frac{1}{x} \cr & \Rightarrow \,\,x = \sqrt 3 \cr & \therefore \,\,BC = BP + PQ + QC \cr & = x + 2 + x = 2 + 2\sqrt 3 \cr & \therefore \,\,{\text{Area of }}\Delta ABC = \frac{{\sqrt 3 }}{4} \times {\left( {2 + 2\sqrt 3 } \right)^2} \cr & = 4\sqrt 3 + 6\,\,{\text{sq}}{\text{. units}}{\text{.}} \cr} $$