Question
In an electrical circuit $$R,L,C$$ and an $$a.c.$$ voltage source are all connected in series. When $$L$$ is removed from the circuit, the phase difference between the voltage the current in the circuit is $$\frac{\pi }{3}.$$ If instead, $$C$$ is removed from the circuit, the phase difference is again $$\frac{\pi }{3}.$$ The power factor of the circuit is :
A.
$$\frac{1}{2}$$
B.
$$\frac{1}{{\sqrt 2 }}$$
C.
1
D.
$$\frac{{\sqrt 3 }}{2}$$
Answer :
1
Solution :
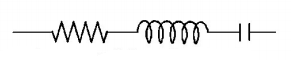
when $$L$$ is removed from the circuit
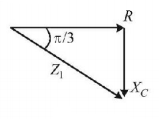
$$\eqalign{ & \frac{{{X_C}}}{R} = \tan \frac{\pi }{3} \cr & {X_C} = R\tan \frac{\pi }{3}\,......\left( {\text{i}} \right) \cr} $$
when $$C$$ is remove from the circuit
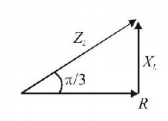
$$\eqalign{ & \frac{{{X_L}}}{R} = \tan \frac{\pi }{3} \cr & {X_C} = R\tan \frac{\pi }{3}\,......\left( {{\text{ii}}} \right) \cr} $$
net impedence $$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} = R$$
power factor $$\cos \phi = \frac{R}{Z} = 1$$

when $$L$$ is removed from the circuit

$$\eqalign{ & \frac{{{X_C}}}{R} = \tan \frac{\pi }{3} \cr & {X_C} = R\tan \frac{\pi }{3}\,......\left( {\text{i}} \right) \cr} $$
when $$C$$ is remove from the circuit

$$\eqalign{ & \frac{{{X_L}}}{R} = \tan \frac{\pi }{3} \cr & {X_C} = R\tan \frac{\pi }{3}\,......\left( {{\text{ii}}} \right) \cr} $$
net impedence $$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} = R$$
power factor $$\cos \phi = \frac{R}{Z} = 1$$