Question
In a Wheatstone bridge resistance of each of the four sides is $$10\,\Omega .$$ If the resistance of the galvanometer is also $$10\,\Omega ,$$ then effective resistance of the bridge will be
A.
$$10\,\Omega $$
B.
$$5\,\Omega $$
C.
$$20\,\Omega $$
D.
$$40\,\Omega $$
Answer :
$$10\,\Omega $$
Solution :
The given circuit can be shown as,
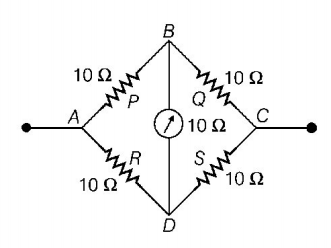
From figure, $$\frac{P}{Q} = \frac{{10}}{{10}} = 1$$
$$\eqalign{ & \frac{R}{S} = \frac{{10}}{{10}} = 1 \cr & \therefore \frac{P}{Q} = \frac{R}{S} \cr} $$
Hence, Wheatstone bridge is balanced. Therefore, the galvanometer will be ineffective. The above Wheatstone bridge can be redrawn as
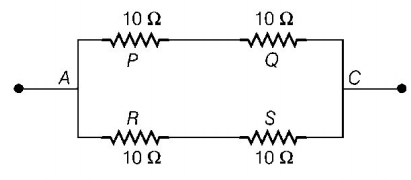
Resistances $$P$$ and $$Q$$ are in series, so
$$R' = 10 + 10 = 20\,\Omega $$
Resistances $$R$$ and $$S$$ are in series, so
$$R'' = 10 + 10 = 20\,\Omega $$
Now, $${R'}$$ and $${R''}$$ are in parallel hence, net resistance of the circuit
$$ = \frac{{R' \times R''}}{{R' + R''}} = \frac{{20 \times 20}}{{20 + 20}} = 10\,\Omega $$
The given circuit can be shown as,

From figure, $$\frac{P}{Q} = \frac{{10}}{{10}} = 1$$
$$\eqalign{ & \frac{R}{S} = \frac{{10}}{{10}} = 1 \cr & \therefore \frac{P}{Q} = \frac{R}{S} \cr} $$
Hence, Wheatstone bridge is balanced. Therefore, the galvanometer will be ineffective. The above Wheatstone bridge can be redrawn as

Resistances $$P$$ and $$Q$$ are in series, so
$$R' = 10 + 10 = 20\,\Omega $$
Resistances $$R$$ and $$S$$ are in series, so
$$R'' = 10 + 10 = 20\,\Omega $$
Now, $${R'}$$ and $${R''}$$ are in parallel hence, net resistance of the circuit
$$ = \frac{{R' \times R''}}{{R' + R''}} = \frac{{20 \times 20}}{{20 + 20}} = 10\,\Omega $$
