Question
In a Wheatstone bridge, all the four arms have equal resistance $$R.$$ If the resistance of the galvanometer arm is also $$R,$$ the equivalent resistance of the combination as seen by the battery is
A.
$$R$$
B.
$$2\,R$$
C.
$$\frac{R}{4}$$
D.
$$\frac{R}{2}$$
Answer :
$$R$$
Solution :
$$\frac{{{R_{AB}}}}{{{R_{BC}}}} = \frac{{{R_{AD}}}}{{{R_{DC}}}}$$
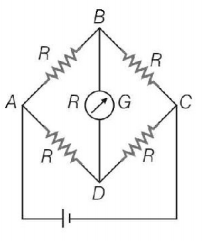
As bridge is in balanced condition, no current will flow through $$BD.$$
$$\eqalign{ & {R_1} = {R_{AB}} + {R_{BC}} \cr & = R + R \cr & = 2\,R \cr & {R_2} = {R_{AD}} + {R_{CD}} \cr & = R + R \cr & = 2\,R \cr} $$
$${R_1}$$ and $${R_2}$$ are in parallel combination.
Hence, equivalent resistance between $$A$$ and $$C$$ will be
$$\therefore {R_{{\text{eq}}}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{4{R^2}}}{{4R}} = R$$
$$\frac{{{R_{AB}}}}{{{R_{BC}}}} = \frac{{{R_{AD}}}}{{{R_{DC}}}}$$

As bridge is in balanced condition, no current will flow through $$BD.$$
$$\eqalign{ & {R_1} = {R_{AB}} + {R_{BC}} \cr & = R + R \cr & = 2\,R \cr & {R_2} = {R_{AD}} + {R_{CD}} \cr & = R + R \cr & = 2\,R \cr} $$
$${R_1}$$ and $${R_2}$$ are in parallel combination.
Hence, equivalent resistance between $$A$$ and $$C$$ will be
$$\therefore {R_{{\text{eq}}}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{4{R^2}}}{{4R}} = R$$
