In a $$\vartriangle ABC,B = {90^ \circ },AC = h$$      and the length of the perpendicular from $$B$$ to $$AC$$  is $$p$$ such that $$h = 4p.$$  If $$AB < BC$$   then $$\angle C$$ has the measure

Solution :

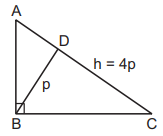
Here, $$CD = p\cot C\,\,{\text{and }}AD = p\cot A = p\tan C$$
Adding, $$4p = p\cot C + p\tan C$$
$$\eqalign{ & \Rightarrow \,\,\tan C + \cot C = 4 \cr & {\text{or, }}\frac{1}{{\sin C \cdot \cos C}} = 4\,\,{\text{or, }}\sin 2C = \frac{1}{2} \cr & \Rightarrow \,\,C = {15^ \circ }. \cr} $$