Question
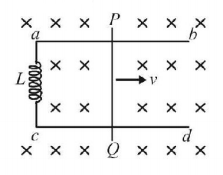
In a uniform and constant magnetic field of induction $$B,$$ two long conducting wires $$ab$$ and $$cd$$ are kept parallel to each other at distance $$\ell $$ with their plane perpendicular to $$B.$$ The ends $$a$$ and $$c$$ are connected together by an ideal inductor of inductance $$L.$$ A conducting slider wire $$PQ$$ is imparted a speed $${v_0}$$ at time $$t = 0.$$ The situation is shown in the figure.
In a uniform and constant magnetic field of induction $$B,$$ two long conducting wires $$ab$$ and $$cd$$ are kept parallel to each other at distance $$\ell $$ with their plane perpendicular to $$B.$$ The ends $$a$$ and $$c$$ are connected together by an ideal inductor of inductance $$L.$$ A conducting slider wire $$PQ$$ is imparted a speed $${v_0}$$ at time $$t = 0.$$ The situation is shown in the figure.
At time $$t = \frac{{\pi \sqrt {mL} }}{{4B\ell }},$$ the value of current $$I$$ through the wire $$PQ$$ is (ignore any resistance, electrical as well as mechanical)
A.
$$\sqrt {\frac{{mv_0^2}}{L}} $$
B.
$$\sqrt {\frac{{mv_0^2}}{{2L}}} $$
C.
$$\sqrt {\frac{{mv_0^2}}{{4L}}} $$
D.
zero.
Answer :
$$\sqrt {\frac{{mv_0^2}}{{2L}}} $$
Solution :
$$\eqalign{ & I\left( t \right) = \sqrt {\frac{m}{L}} {v_0}\sin \omega t\,\,{\text{where}}\,\,\omega = \frac{{B\ell }}{{\sqrt {mL} }} \cr & \Rightarrow I = \sqrt {\frac{{mv_0^2}}{{2L}}} \cr} $$
$$\eqalign{ & I\left( t \right) = \sqrt {\frac{m}{L}} {v_0}\sin \omega t\,\,{\text{where}}\,\,\omega = \frac{{B\ell }}{{\sqrt {mL} }} \cr & \Rightarrow I = \sqrt {\frac{{mv_0^2}}{{2L}}} \cr} $$
