Question
In a resonance tube with tuning fork of frequency $$512\,Hz,$$ first resonance occurs at water level equal to $$30.3\,cm$$ and second resonance occurs at $$63.7\,cm.$$ The maximum possible error in the speed of sound is
A.
$$51.2\,cm/s$$
B.
$$102.4\,cm/s$$
C.
$$204.8\,cm/s$$
D.
$$153.6\,cm/s$$
Answer :
$$204.8\,cm/s$$
Solution :
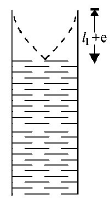
For first resonance
$${\ell _1} + e = \frac{\lambda }{4}$$
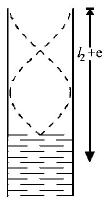
For second resonance
$${\ell _2} + e = \frac{{3\,\lambda }}{4}$$
$$\eqalign{ & {\text{But, }}\nu = \nu \lambda \cr & \therefore \,\,\nu = \nu \frac{4}{3}\left( {{\ell _2} + e} \right) \cr & \Rightarrow \,\,{\ell _2} + e = \frac{{3\nu }}{{4\nu }}\,\,\,.....\left( {\text{i}} \right) \cr & \therefore \,\,\nu = \nu 4\left( {{\ell _1} + e} \right) \cr & \Rightarrow \,\,{\ell _1} + e = \frac{\nu }{{4\nu }}\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
Subtracting (i) and (ii),
$$\eqalign{ & \nu = 2\nu \left( {{\ell _2} - {\ell _1}} \right) \cr & \therefore \,\,\Delta \nu = 2\nu \left( {\Delta {\ell _2} + \Delta {\ell _1}} \right) \cr & = 2 \times 512 \times \left( {0.1 + 0.1} \right)\,cm/s \cr & = 204.8\,cm/s \cr} $$

For first resonance
$${\ell _1} + e = \frac{\lambda }{4}$$

For second resonance
$${\ell _2} + e = \frac{{3\,\lambda }}{4}$$
$$\eqalign{ & {\text{But, }}\nu = \nu \lambda \cr & \therefore \,\,\nu = \nu \frac{4}{3}\left( {{\ell _2} + e} \right) \cr & \Rightarrow \,\,{\ell _2} + e = \frac{{3\nu }}{{4\nu }}\,\,\,.....\left( {\text{i}} \right) \cr & \therefore \,\,\nu = \nu 4\left( {{\ell _1} + e} \right) \cr & \Rightarrow \,\,{\ell _1} + e = \frac{\nu }{{4\nu }}\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
Subtracting (i) and (ii),
$$\eqalign{ & \nu = 2\nu \left( {{\ell _2} - {\ell _1}} \right) \cr & \therefore \,\,\Delta \nu = 2\nu \left( {\Delta {\ell _2} + \Delta {\ell _1}} \right) \cr & = 2 \times 512 \times \left( {0.1 + 0.1} \right)\,cm/s \cr & = 204.8\,cm/s \cr} $$