If water is poured into an inverted hollow cone whose semi-vertical angle is $${30^ \circ }.$$  Its depth (measured along the axis) increases at the rate of $$1\,cm/s.$$  The rate at which the volume of water increases when the depth is $$24\,cm$$  is :

Solution :

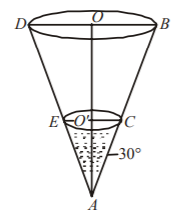
Let $$A$$ be the vertex and $$AO$$  the axis of the cone.
Let $$O'A = h$$   be the depth of water in the cone.
$$\eqalign{ & {\text{In}}\Delta AO'C, \cr & \tan \,{30^ \circ } = \frac{{O'C}}{h}{\text{ or }}O'C = \frac{h}{{\sqrt 3 }} = {\text{radius}} \cr & V = {\text{Volume of water in the cone}} \cr & = \frac{1}{3}\pi {\left( {O'C} \right)^2} \times AO' \cr & = \frac{1}{3}\pi \left( {\frac{{{h^2}}}{3}} \right) \times h \cr & = \frac{\pi }{9}{h^3} \cr & {\text{or }}\frac{{dV}}{{dt}} = \frac{\pi }{3}{h^2}\frac{{dh}}{{dt}}......\left( 1 \right) \cr} $$
But given that depth of water increases at the rate of $$1\,cm/s.$$
So, $$\frac{{dh}}{{dt}} = 1\,cm/s......\left( 2 \right)$$
From $$\left( 1 \right)$$ and $$\left( 2 \right),\,\,\frac{{dV}}{{dt}} = \frac{{\pi {h^2}}}{3}$$
When $$h = 24\,cm,$$   the rate of increase of volume is $$\frac{{dV}}{{dt}} = \frac{{\pi {{\left( {24} \right)}^2}}}{3} = 192\,c{m^3}/s.$$