Question
If $${\theta _1}$$ and $${\theta _2}$$ be the apparent angles of dip observed in two vertical planes at right angles to each other, then the true angle of dip $$\theta $$ is given by
A.
$${\cot ^2}\theta = {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2}$$
B.
$${\tan ^2}\theta = {\tan ^2}{\theta _1} + {\tan ^2}{\theta _2}$$
C.
$${\cot ^2}\theta = {\cot ^2}{\theta _1} - {\cot ^2}{\theta _2}$$
D.
$${\tan ^2}\theta = {\tan ^2}{\theta _1} - {\tan ^2}{\theta _2}$$
Answer :
$${\cot ^2}\theta = {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2}$$
Solution :
Let the $${B_H}$$ and $${B_V}$$ be the horizontal and vertical component of earth’s magnetic field $$B.$$
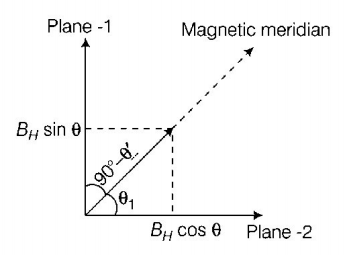
$$\tan \theta = \frac{{{B_V}}}{{{B_H}}} \Rightarrow \cot \theta = \frac{{{B_H}}}{{{B_V}}}\,......\left( {\text{i}} \right)$$
Let, plane 1 and 2 are mutually perpendicular planes making angle $$\theta $$ and $$\left( {{{90}^ \circ } - \theta } \right)$$ with magnetic meridian. The vertical component of earth of earth's magnetic field remain same in two plane but effective horizontal components in the two planes is given by
$$\eqalign{ & {B_1} = {B_H}\cos \theta '\,\,......\left( {{\text{ii}}} \right) \cr & {\text{and}}\,\,{B_2} = {B_H}\sin \theta '\,\,......\left( {{\text{iii}}} \right) \cr & {\text{Then,}}\,\,\tan {\theta _1} = \frac{{{B_V}}}{{{B_1}}} = \frac{{{B_V}}}{{{B_H}\cos \theta '}} \cr & \cot {\theta _1} = \frac{{{B_H}\cos \theta '}}{{{B_V}}}\,......\left( {{\text{iv}}} \right) \cr} $$
Similarly,
$$\eqalign{ & \Rightarrow \tan {\theta _2} = \frac{{{B_V}}}{{{B_2}}} = \frac{{{B_V}}}{{{B_H}\sin \theta '}} \cr & \Rightarrow \cot {\theta _2} = \frac{{{B_H}\sin \theta '}}{{{B_V}}}\,......\left( {\text{v}} \right) \cr} $$
From Eq. (iv) and Eq. (v)
$$\eqalign{ & \Rightarrow {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2} = \frac{{B_H^2{{\cos }^2}\theta '}}{{B_V^2}} + \frac{{B_H^2{{\sin }^2}\theta '}}{{B_V^2}} \cr & \Rightarrow {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2} = \frac{{B_H^2}}{{B_V^2}}\left( {{{\cos }^2}\theta ' + {{\sin }^2}\theta '} \right) \cr & \Rightarrow {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2} = {\cot ^2}\theta \cr} $$
Let the $${B_H}$$ and $${B_V}$$ be the horizontal and vertical component of earth’s magnetic field $$B.$$

$$\tan \theta = \frac{{{B_V}}}{{{B_H}}} \Rightarrow \cot \theta = \frac{{{B_H}}}{{{B_V}}}\,......\left( {\text{i}} \right)$$
Let, plane 1 and 2 are mutually perpendicular planes making angle $$\theta $$ and $$\left( {{{90}^ \circ } - \theta } \right)$$ with magnetic meridian. The vertical component of earth of earth's magnetic field remain same in two plane but effective horizontal components in the two planes is given by
$$\eqalign{ & {B_1} = {B_H}\cos \theta '\,\,......\left( {{\text{ii}}} \right) \cr & {\text{and}}\,\,{B_2} = {B_H}\sin \theta '\,\,......\left( {{\text{iii}}} \right) \cr & {\text{Then,}}\,\,\tan {\theta _1} = \frac{{{B_V}}}{{{B_1}}} = \frac{{{B_V}}}{{{B_H}\cos \theta '}} \cr & \cot {\theta _1} = \frac{{{B_H}\cos \theta '}}{{{B_V}}}\,......\left( {{\text{iv}}} \right) \cr} $$
Similarly,
$$\eqalign{ & \Rightarrow \tan {\theta _2} = \frac{{{B_V}}}{{{B_2}}} = \frac{{{B_V}}}{{{B_H}\sin \theta '}} \cr & \Rightarrow \cot {\theta _2} = \frac{{{B_H}\sin \theta '}}{{{B_V}}}\,......\left( {\text{v}} \right) \cr} $$
From Eq. (iv) and Eq. (v)
$$\eqalign{ & \Rightarrow {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2} = \frac{{B_H^2{{\cos }^2}\theta '}}{{B_V^2}} + \frac{{B_H^2{{\sin }^2}\theta '}}{{B_V^2}} \cr & \Rightarrow {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2} = \frac{{B_H^2}}{{B_V^2}}\left( {{{\cos }^2}\theta ' + {{\sin }^2}\theta '} \right) \cr & \Rightarrow {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2} = {\cot ^2}\theta \cr} $$