Question
If the two circles $${\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = {r^2}$$ and $${x^2} + {y^2} - 8x + 2y + 8 = 0$$ intersect in two distinct points, then-
A.
$$2 < r < 8$$
B.
$$r < 2$$
C.
$$r = 2$$
D.
$$r > 2$$
Answer :
$$2 < r < 8$$
Solution :
We have two circles $${\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = {r^2}$$
Centre (1, 3), radius $$=r$$
and $${x^2} + {y^2} - 8x + 2y + 8 = 0$$
Centre $$\left( {4,\, - 1} \right),$$ radius $$ = \sqrt {16 + 1 - 8} = 3$$
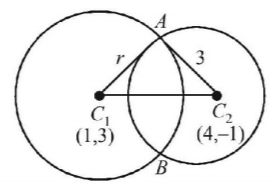
As the two circles intersect each other in two distinct points we should have
$$\eqalign{ & {C_1}{C_2} < {r_1} + {r_2}\,\,\,\,\,{\text{and}}\,\,\,\,\,\,{C_1}{C_2} > \left| {{r_1} - {r_2}} \right| \cr & \Rightarrow {C_1}{C_2} < r + 3\,\,\,\,\,{\text{and}}\,\,\,\,\,\,{C_1}{C_2} < \left| {{r_1} - {r_2}} \right| \cr & \Rightarrow \sqrt {9 + 16} < r + 3\,\,\,\,\,{\text{and}}\,\,\,\,\,\,5 > \left| {r - 3} \right| \cr & \Rightarrow 5 < r + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \left| {r - 3} \right| < 5 \cr & \Rightarrow r > 2.....({\text{i}})\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow - 5 < r - 3 < 5 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow - 2 < r < 8.....({\text{ii}}) \cr} $$
Combining (i) and (ii), we get
$$2 < r < 8$$
We have two circles $${\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = {r^2}$$
Centre (1, 3), radius $$=r$$
and $${x^2} + {y^2} - 8x + 2y + 8 = 0$$
Centre $$\left( {4,\, - 1} \right),$$ radius $$ = \sqrt {16 + 1 - 8} = 3$$

As the two circles intersect each other in two distinct points we should have
$$\eqalign{ & {C_1}{C_2} < {r_1} + {r_2}\,\,\,\,\,{\text{and}}\,\,\,\,\,\,{C_1}{C_2} > \left| {{r_1} - {r_2}} \right| \cr & \Rightarrow {C_1}{C_2} < r + 3\,\,\,\,\,{\text{and}}\,\,\,\,\,\,{C_1}{C_2} < \left| {{r_1} - {r_2}} \right| \cr & \Rightarrow \sqrt {9 + 16} < r + 3\,\,\,\,\,{\text{and}}\,\,\,\,\,\,5 > \left| {r - 3} \right| \cr & \Rightarrow 5 < r + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \left| {r - 3} \right| < 5 \cr & \Rightarrow r > 2.....({\text{i}})\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow - 5 < r - 3 < 5 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow - 2 < r < 8.....({\text{ii}}) \cr} $$
Combining (i) and (ii), we get
$$2 < r < 8$$