Question
If the roots of the equation $${x^2} - 2ax + {a^2} + a - 3 = 0$$ are real and less than 3, then
A.
$$a < 2$$
B.
$$2 \leqslant a \leqslant 3$$
C.
$$3 < a \leqslant 4$$
D.
$$a > 4$$
Answer :
$$a < 2$$
Solution :
KEY CONCEPT : If both roots of a quadratic equation
$$a{x^2} + bx + c = 0$$ are less than $$k$$
then $$af\left( k \right) > 0,D \geqslant 0,\alpha + \beta < 2k.$$
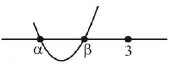
$$\eqalign{ & f\left( x \right) = {x^2} - 2ax + {a^2} + a - 3 = 0, \cr & f\left( 3 \right) > 0,\alpha + \beta < 6,D \geqslant 0. \cr & \Rightarrow \,\,{a^2} - 5a + 6 > 0,a < 3, - 4a + 12 \geqslant 0 \cr & \Rightarrow \,\,a < 2\,\,{\text{or }}a > 3,a < 3,a < 3 \cr & \Rightarrow \,\,a < 2. \cr} $$
KEY CONCEPT : If both roots of a quadratic equation
$$a{x^2} + bx + c = 0$$ are less than $$k$$
then $$af\left( k \right) > 0,D \geqslant 0,\alpha + \beta < 2k.$$

$$\eqalign{ & f\left( x \right) = {x^2} - 2ax + {a^2} + a - 3 = 0, \cr & f\left( 3 \right) > 0,\alpha + \beta < 6,D \geqslant 0. \cr & \Rightarrow \,\,{a^2} - 5a + 6 > 0,a < 3, - 4a + 12 \geqslant 0 \cr & \Rightarrow \,\,a < 2\,\,{\text{or }}a > 3,a < 3,a < 3 \cr & \Rightarrow \,\,a < 2. \cr} $$