Question
If the ordinate $$x = a$$ divides the area bounded by $$x$$-axis, part of the curve $$y = 1 + \frac{8}{{{x^2}}}$$ and the ordinates $$x = 2,\,x = 4$$ into two equal parts, then $$a$$ is equal to :
A.
$$\sqrt 2 $$
B.
$$2\sqrt 2 $$
C.
$$3\sqrt 2 $$
D.
None of these
Answer :
$$2\sqrt 2 $$
Solution :
The area bounded by the curve $$y = 1 + \frac{8}{{{x^2}}},\,\,x$$ -axis and the ordinates $$x = 2,\,x = 4$$ is
$$\eqalign{ & = \int_2^4 {y\,dx} \cr & = \int_2^4 {\left( {1 + \frac{8}{{{x^2}}}} \right)dx} \cr & = \left[ {x - \frac{8}{x}} \right]_2^4 \cr & = 4 \cr} $$
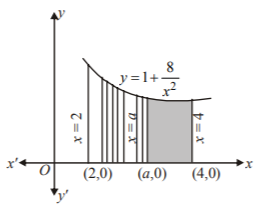
Since, $$x = a$$ divides this area into two equal parts.
$$\therefore $$ Required area $$ = 2\int_2^a {y\,dx} $$
$$\eqalign{ & \therefore \,4 = 2\int_2^a {\left( {1 + \frac{8}{{{x^2}}}} \right)dx} \cr & \Rightarrow 2 = \left[ {x - \frac{8}{x}} \right]_2^a \cr & \Rightarrow 2 = \left( {a - \frac{8}{a}} \right) - \left( {2 - 4} \right) \cr & \Rightarrow {a^2} = 8 \cr & \therefore \,a = 2\sqrt 2 \cr} $$
The area bounded by the curve $$y = 1 + \frac{8}{{{x^2}}},\,\,x$$ -axis and the ordinates $$x = 2,\,x = 4$$ is
$$\eqalign{ & = \int_2^4 {y\,dx} \cr & = \int_2^4 {\left( {1 + \frac{8}{{{x^2}}}} \right)dx} \cr & = \left[ {x - \frac{8}{x}} \right]_2^4 \cr & = 4 \cr} $$

Since, $$x = a$$ divides this area into two equal parts.
$$\therefore $$ Required area $$ = 2\int_2^a {y\,dx} $$
$$\eqalign{ & \therefore \,4 = 2\int_2^a {\left( {1 + \frac{8}{{{x^2}}}} \right)dx} \cr & \Rightarrow 2 = \left[ {x - \frac{8}{x}} \right]_2^a \cr & \Rightarrow 2 = \left( {a - \frac{8}{a}} \right) - \left( {2 - 4} \right) \cr & \Rightarrow {a^2} = 8 \cr & \therefore \,a = 2\sqrt 2 \cr} $$