If the middle points of sides $$BC,\,CA\,\& \,AB$$    of triangle $$ABC$$  are respectively $$D,\,E,\,F$$   then position vector of centre of triangle $$DEF,$$  when position vector of $$A,\,B,\,C$$   are respectively $$\hat i + \hat j,\,\hat j + \hat k,\,\hat k + \hat i$$     is :

Solution :

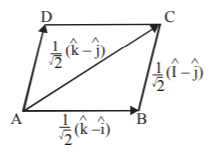
The position vector of points $$D,\,E,\,F$$   are respectively
$$\frac{{\hat i + \hat j}}{2} + \hat k,\,\hat i + \frac{{\hat k + \hat j}}{2}{\text{ and }}\frac{{\hat i + \hat k}}{2} + \hat j$$
So, position vector of centre of $$\Delta DEF$$
$$\eqalign{ & = \frac{1}{3}\left[ {\frac{{\hat i + \hat j}}{2} + \hat k + \hat i + \frac{{\hat k + \hat j}}{2}{\text{ + }}\frac{{\hat i + \hat k}}{2} + \hat j} \right] \cr & = \frac{2}{3}\left[ {\hat i + \hat j + \hat k} \right] \cr} $$