Question
If the equation of the common tangent at the point $$\left( {1,\, - 1} \right)$$ to the two circles, each of radius $$13,$$ is $$12x + 5y - 7 = 0$$ then the centers of the two circles are :
A.
$$\left( {13,\,4} \right)\left( { - 11,\,6} \right)$$
B.
$$\left( {13,\,4} \right)\left( { - 11,\, - 6} \right)$$
C.
$$\left( {13,\, - 4} \right)\left( { - 11,\, - 6} \right)$$
D.
$$\left( { - 13,\,4} \right)\left( { - 11,\, - 6} \right)$$
Answer :
$$\left( {13,\,4} \right)\left( { - 11,\, - 6} \right)$$
Solution :
Let $$A,\,B,$$ be the centers of the two circles,
Slope of the common tangent $$ = - \frac{{12}}{5}$$
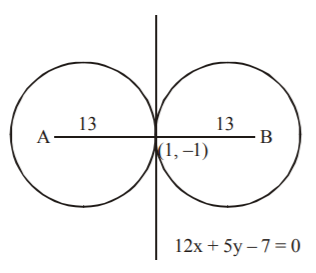
$$\therefore $$ Slope of $$AB$$ is $$\tan \,\theta = - \frac{1}{{ - \frac{{12}}{5}}} = \frac{5}{{12}}$$
The point $$\left( {1,\, - 1} \right)$$ lies on the line $$AB$$ and the points $$A$$ and $$B$$ are at a distance $$13$$ from the point $$\left( {1,\, - 1} \right)$$
$$\therefore $$ Coordinates of $$A$$ and $$B$$ are $$\left( {1 \pm 13\,\cos \,\theta ,\, - 1 \pm 13\,\sin \,\theta } \right),$$ where $$\tan \,\theta = \frac{5}{{12}}$$
$$\eqalign{ & {\text{i}}{\text{.e}}{\text{.,}}\,\,\left( {1 \pm 13\frac{{12}}{{13}},\, - 1 \pm 13\frac{5}{{13}}} \right){\text{ or }}\left( {1 \pm 12,\, - 1 \pm 5} \right) \cr & {\text{i}}{\text{.e}}{\text{.,}}\,\,\left( {13,\,4} \right){\text{ and }}\left( { - 11,\, - 6} \right) \cr} $$
Let $$A,\,B,$$ be the centers of the two circles,
Slope of the common tangent $$ = - \frac{{12}}{5}$$
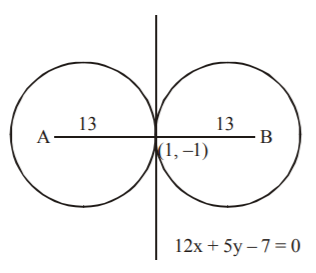
$$\therefore $$ Slope of $$AB$$ is $$\tan \,\theta = - \frac{1}{{ - \frac{{12}}{5}}} = \frac{5}{{12}}$$
The point $$\left( {1,\, - 1} \right)$$ lies on the line $$AB$$ and the points $$A$$ and $$B$$ are at a distance $$13$$ from the point $$\left( {1,\, - 1} \right)$$
$$\therefore $$ Coordinates of $$A$$ and $$B$$ are $$\left( {1 \pm 13\,\cos \,\theta ,\, - 1 \pm 13\,\sin \,\theta } \right),$$ where $$\tan \,\theta = \frac{5}{{12}}$$
$$\eqalign{ & {\text{i}}{\text{.e}}{\text{.,}}\,\,\left( {1 \pm 13\frac{{12}}{{13}},\, - 1 \pm 13\frac{5}{{13}}} \right){\text{ or }}\left( {1 \pm 12,\, - 1 \pm 5} \right) \cr & {\text{i}}{\text{.e}}{\text{.,}}\,\,\left( {13,\,4} \right){\text{ and }}\left( { - 11,\, - 6} \right) \cr} $$