Question
If the curves $${y^2} = 6x,\,9{x^2} + b{y^2} = 16$$ intersect each other at right angles, then the value of $$b$$ is :
A.
$$\frac{7}{2}$$
B.
4
C.
$$\frac{9}{2}$$
D.
6
Answer :
$$\frac{9}{2}$$
Solution :
Let curve intersect each other at point $$P\left( {{x_1},{y_1}} \right)$$
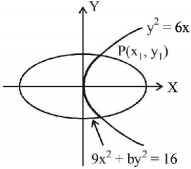
Since, point of intersection is on both the curves, then
$$y_1^2 = 6{x_1}\,......\left( {\text{i}} \right)\,\,\,\,\,{\text{and}}\,9x_1^2 + by_1^2 = 16\,......\left( {{\text{ii}}} \right)$$
Now, find the slope of tangent to both the curves at the point of intersection $$P\left( {{x_1},{y_1}} \right)$$
For slope of curves:
curve (i):
$${\left( {\frac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = {m_1} = \frac{3}{{{y_1}}}$$
curve (ii):
$${\text{and}}\,{\left( {\frac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = {m_2} = - \frac{{9{x_1}}}{{b{y_1}}}$$
Since, both the curves intersect each other at right angle then,
$$\eqalign{ & {m_1}{m_2} = - 1 \Rightarrow \frac{{27{x_1}}}{{by_{_1}^2}} = 1 \Rightarrow b = 27\frac{{{x_1}}}{{y_{_1}^2}} \cr & \therefore \,\,{\text{from}}\,{\text{equation}}\,\left( {\text{i}} \right),\,b = 27 \times \frac{1}{6} = \frac{9}{2} \cr} $$
Let curve intersect each other at point $$P\left( {{x_1},{y_1}} \right)$$

Since, point of intersection is on both the curves, then
$$y_1^2 = 6{x_1}\,......\left( {\text{i}} \right)\,\,\,\,\,{\text{and}}\,9x_1^2 + by_1^2 = 16\,......\left( {{\text{ii}}} \right)$$
Now, find the slope of tangent to both the curves at the point of intersection $$P\left( {{x_1},{y_1}} \right)$$
For slope of curves:
curve (i):
$${\left( {\frac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = {m_1} = \frac{3}{{{y_1}}}$$
curve (ii):
$${\text{and}}\,{\left( {\frac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = {m_2} = - \frac{{9{x_1}}}{{b{y_1}}}$$
Since, both the curves intersect each other at right angle then,
$$\eqalign{ & {m_1}{m_2} = - 1 \Rightarrow \frac{{27{x_1}}}{{by_{_1}^2}} = 1 \Rightarrow b = 27\frac{{{x_1}}}{{y_{_1}^2}} \cr & \therefore \,\,{\text{from}}\,{\text{equation}}\,\left( {\text{i}} \right),\,b = 27 \times \frac{1}{6} = \frac{9}{2} \cr} $$